【2024神戸大学・文系・第１問】3次関数の最小値、対数型の漸化式

解答・解説

(１)　\(a_{1}\) と \(b_{1}\) を求めよ．

\(y=\displaystyle\frac{1}{3}x^3-10x\) より

\(y^{\prime}=x^2-10\)

\(x≧0\) における増減表は下のようになるため

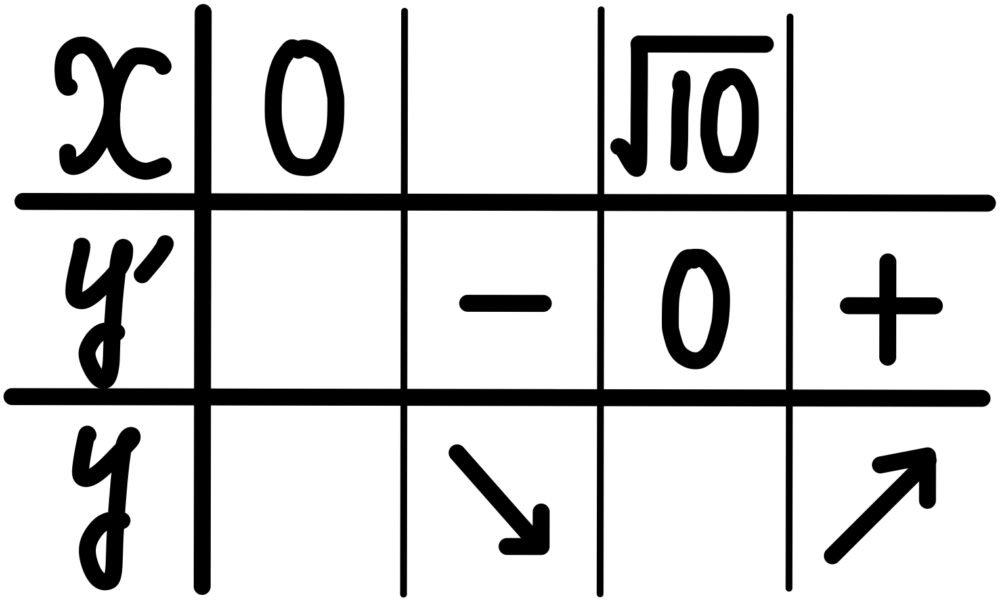
\(x=\sqrt{10}\) で最小値をとる．

よって，\(a_{1}=\sqrt{10}\)

また，\(b_{1}=\log_{10}{\sqrt{10}}=\displaystyle\frac{1}{2}\)

(２)　\(a_{n+1}\) を \(a_{n}\) を用いて表せ．

\(y=\displaystyle\frac{1}{3}x^3-10a_{n}x\) より

\(y^{\prime}=x^2-10a_{n}\)

\(x≧0\) における増減表は下のようになるため

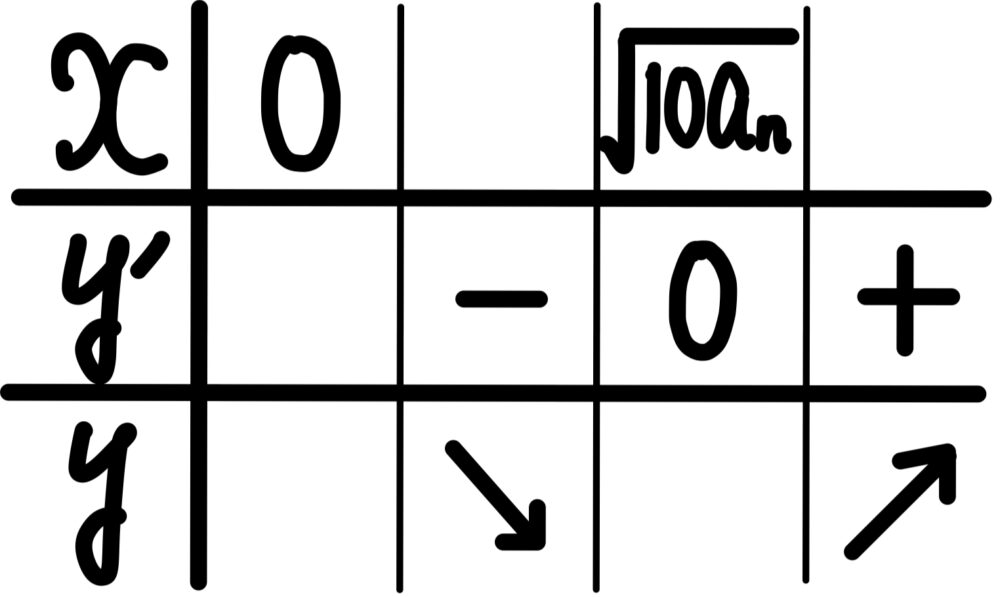
\(x=\sqrt{10a_{n}}\) で最小値をとる．

よって，\(a_{n+1}=\sqrt{10a_{n}}\)

(３)　\(b_{n+1}\) を \(b_{n}\) を用いて表せ．

(２)の結果から

\(\log_{10}{a_{n+1}}=\log_{10}{\sqrt{10a_{n}}}=\displaystyle\frac{1}{2}\left(1+\log_{10}{a_{n}}\right)\) より

\(b_{n+1}=\displaystyle\frac{1}{2}\left(b_{n}+1\right)\)

(４)　数列 \(\left\{b_{n}\right\}\) の一般項を求めよ．

(３)の結果より

\(b_{n+1}-1=\displaystyle\frac{1}{2}\left(b_{n}-1\right)\)

数列 \(\left\{b_{n}-1\right\}\) は初項が \(b_{1}-1=-\displaystyle\frac{1}{2}\) ，公比が \(\displaystyle\frac{1}{2}\) の等比数列であるから

\(b_{n}-1=-\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{2}\right)^{n-1}\)

よって，\(b_{n}=-\left(\displaystyle\frac{1}{2}\right)^n+1\)

(５)　\(\displaystyle\frac{a_{1}a_{2}a_{3}}{100}\) の値を求めよ．

(４)の結果より

\(b_{1}+b_{2}+b_{3}=-\displaystyle\frac{1}{2}-\displaystyle\frac{1}{4}-\displaystyle\frac{1}{8}+3=\displaystyle\frac{17}{8}\)

\(\log_{10}{a_{1}}+\log_{10}{a_{2}}+\log_{10}{a_{3}}=\displaystyle\frac{17}{8}\)

\(\log_{10}{a_{1}a_{2}a_{3}}=\displaystyle\frac{17}{8}\)

\(a_{1}a_{2}a_{3}=10^{\frac{17}{8}}\)

したがって，\(\displaystyle\frac{ a_{1}a_{2}a_{3}}{100}=10^{\frac{1}{8}}\)