3次関数の対称性の証明｜変曲点に関して対称なグラフ

\(3\) 次関数 \(f(x)=ax^3+bx^2+cx+d\) は \(P\) \(\left(-\displaystyle\frac{b}{3a} , f \left(-\displaystyle\frac{b}{3a}\right)\right)\) に関し点対称なグラフになることを示せ．

考え方【隅関数・奇関数】

偶関数・奇関数について

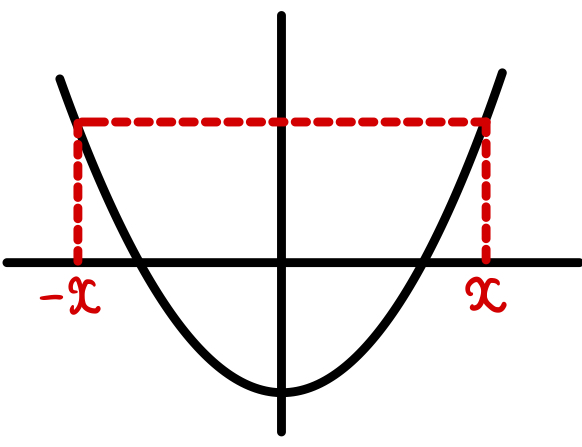
偶関数とは

\(y\) 軸に関して対称なグラフ：\(f(x) = f(-x)\)

例：\(y=3\) (定数関数)、\(y=x^2\)、\(y=\cos x\) など

奇関数とは

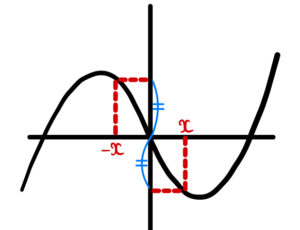
原点に関して対称なグラフ：\(f(-x) = -f(x)\)

例：\(y=x\)、\(y=x^3\)、\(y=\sin x\)、\(y=\tan x\) など

解答

\(p=-\displaystyle\frac{b}{3a}\) とおく．

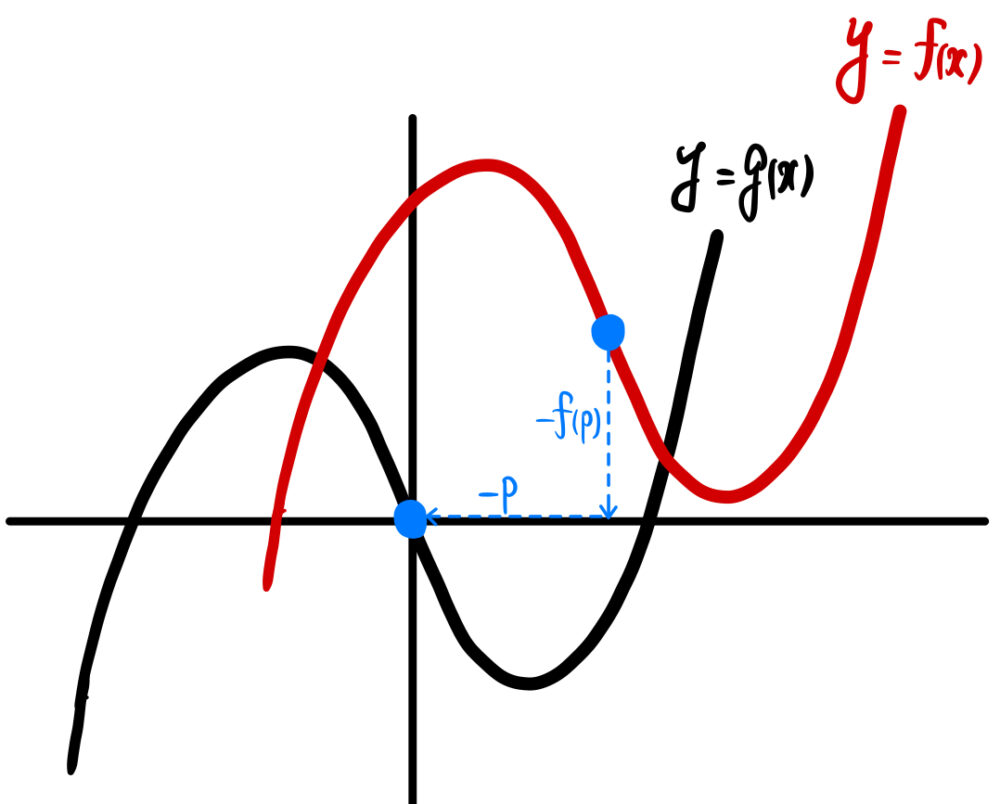
\(y=f(x)\) を \(x\) 軸方向に \(-p\)、\(y\) 軸方向に \(-f(p)\) だけ平行移動すると、

\(y+f(p) = a(x+p)^3+b(x+p)^2+c(x+p)+d\)

\(y+(ap^3+bp^2+cp+d)=a(x^3+3px^2+3p^2x+p^3)+b(x^2+2px+p^2+c(x+p)+d)\)

式をまとめると

\(y=ax^3+(3ap+b)x^2+(3ap^2+2bp+c)x\)

\(p=-\displaystyle\frac{b}{3a}\) より、

\(x^2\) の係数である \(3ap+b=0\)

したがって、\(y=ax^3+(3ap^2+2bp+c)x\)

これを \(g(x)\) とおくと、\(g(-x) = -g(x)\) が成立する．

したがって \(y=g(x)\) は奇関数．

つまり、原点に関して対称なグラフである．

ゆえに、\(y=g(x)\) を \(x\) 軸方向に \(p\)、\(y\) 軸方向に \(f(p)\) だけ平行移動した \(y=f(x)\) のグラフは、 \(P\) \(\left(-\displaystyle\frac{b}{3a} , f \left(-\displaystyle\frac{b}{3a}\right)\right)\) に関し点対称なグラフとなる．

参考【3次関数の変曲点について】

\(3\) 次関数 \(f(x)=ax^3+bx^2+cx+d\) における

\(P\) \(\left(-\displaystyle\frac{b}{3a} , f \left(-\displaystyle\frac{b}{3a}\right)\right)\)

を、「変曲点」という．

点 \(P\) は、\(2\) 階微分を計算することで得られ

\(f^{\prime\prime}(x)=0\) の解が \(x=p\) となる．

\(f(x)=ax^3+bx^2+cx+d\) より

\(f^{\prime}(x)=3ax^2+2bx+c \)

\(f^{\prime \prime}(x)=6ax+2b \)

\(f^{\prime \prime}(x)=0\) より

\(6ax+2b=0\)

\(x=-\displaystyle\frac{b}{3a}\) となる．