【2024神戸大学・理系・第5問】
\(0\) 以上の実数 \(x\) に対して,
\(f(x)=\displaystyle\frac{1}{2}\displaystyle\int^{x}_{-x}\displaystyle\frac{1}{1+u^2}du \)
と定める.以下の問に答えよ.
(1) \(0≦\alpha<\displaystyle\frac{\pi}{2}\) を満たす実数 \(\alpha\) に対して,\(f(\tan\alpha)\) を求めよ.
(2) \(xy\) 平面上で,次の連立不等式の表す領域を図示せよ.
\(0≦x≦1\),\(0≦y≦1\),\(f(x)+f(y)≦f(1)\)
またその領域の面積を求めよ.
解答・解説
(1)
\(f(\tan\alpha)=\displaystyle\frac{1}{2}\displaystyle\int^{\tan\alpha}_{-\tan\alpha}\displaystyle\frac{1}{1+u^2}du \)
\(=\displaystyle\int^{\tan\alpha}_{0}\displaystyle\frac{1}{1+u^2}du \)
\(u=\tan\theta\) とおくと
\(u\):\(0\rightarrow \tan\alpha\) のとき \(\theta\):\(0\rightarrow \alpha\)
また \(du=\displaystyle\frac{1}{\cos^2\theta}d\theta\) より
\( f(\tan\alpha)=\displaystyle\int^{\alpha}_{0}\displaystyle\frac{1}{1+\tan^2\theta}\cdot\displaystyle\frac{1}{\cos^2\theta}d\theta \)
\(=\displaystyle\int^{\alpha}_{0} d\theta \)
\(=\Bigl[\theta\Bigr]^{\alpha}_{0}\)
\(=\alpha\)
(2)
\(0≦x≦1\),\(0≦y≦1\) となる \(x\) ,\(y\) に対し,
\(x=\tan\beta\) \(\left(0≦\beta≦\displaystyle\frac{\pi}{4}\right)\)
\(x=\tan\gamma\) \(\left(0≦\gamma≦\displaystyle\frac{\pi}{4}\right)\)
となる \(\beta\) ,\(\gamma\) が存在する.
(1)の結果より
\(f(x)=f(\tan\beta)=\beta\),\(f(x)=f(\tan\gamma)=\gamma\)
また,\(f(1)=f\left(\tan\displaystyle\frac{\pi}{4}\right)=\displaystyle\frac{\pi}{4}\) で
\(f(x)+f(y)≦f(1)\) より
\(0≦\beta+\gamma≦\displaystyle\frac{\pi}{4}\) ・・・①
①より \(\beta=\gamma=\displaystyle\frac{\pi}{4}\) とはならないため
\(\tan\beta\tan\gamma=xy\not=1\)
\(0≦x≦1\),\(0≦y≦1\) より \(0≦xy<1\) ・・・②
また①より \(0≦\tan(\beta+\gamma)≦1\) であり
\(\tan(\beta+\gamma)=\displaystyle\frac{\tan\beta+\tan\gamma}{1-\tan\beta\tan\gamma}=\displaystyle\frac{x+y}{1-xy}\) より
\(0≦\displaystyle\frac{x+y}{1-xy}≦1\)
②より \(1-xy>0\) であるから
\(0≦x+y≦1-xy\)
\((x+1)y≦-x+1\)
\(x+1>0\) より,\(y≦\displaystyle\frac{-x+1}{x+1}=\displaystyle\frac{2}{x+1}-1\)
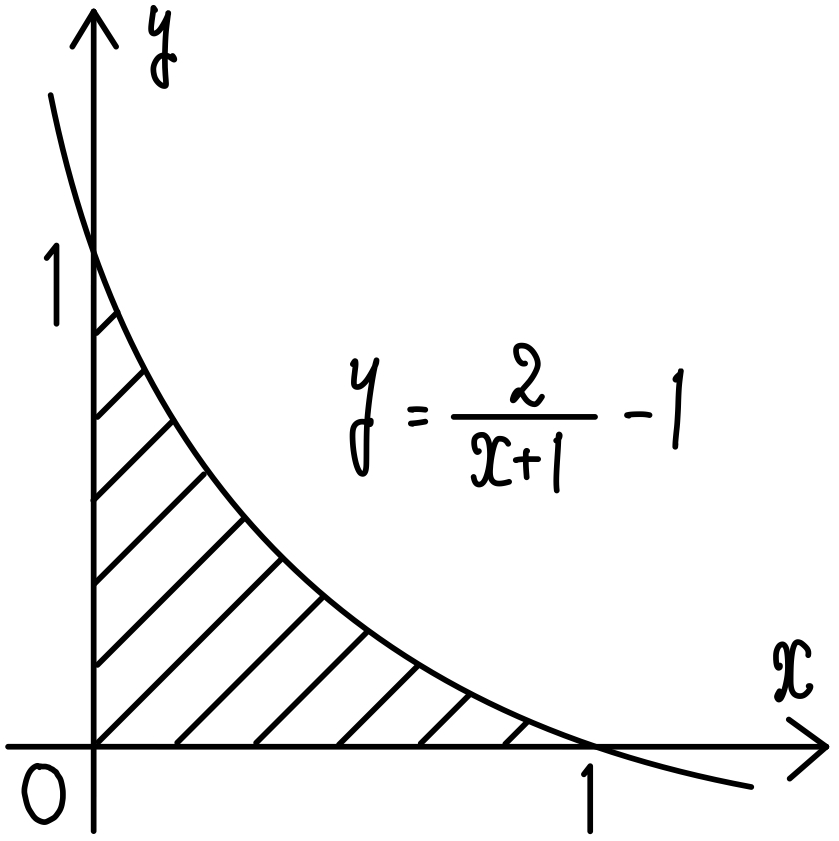 したがって右図の斜線部分が不等式 \(0≦x≦1\),\(0≦y≦1\),\(f(x)+f(y)≦f(1)\) の表す領域である.ただし,境界線を含む.
したがって右図の斜線部分が不等式 \(0≦x≦1\),\(0≦y≦1\),\(f(x)+f(y)≦f(1)\) の表す領域である.ただし,境界線を含む.
また領域の面積を \(S\) とすると
\(S=\displaystyle\int^{1}_{0}\left(\displaystyle\frac{2}{x+1}-1\right)dx\)
\(=\Bigl[2\log{(x+1)}-x\Bigr]^{1}_{0}\)
\(=2\log2-1\)







コメント