【2023京都大学・文理共通・第2問】
空間内の \(4\) 点 \(O\) , \(A\) , \(B\) , \(C\) は同一平面上にないとする.点 \(D\) , \(P\) , \(Q\) を次のように定める.点 \(D\) は \(\overrightarrow{OD}=\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}\) を満たし,点 \(P\) は線分 \(OA\) を \(1\):\(2\) に内分し,点 \(Q\) は線分 \(OB\) の中点である.さらに,直線 \(OD\) 上の点 \(R\) を,直線 \(QR\) と直線 \(PC\) が交点を持つように定める.このとき,線分 \(OR\) の長さと線分 \(RD\) の長さの比 \(OR\):\(RD\) を求めよ.
解答・解説
 直線 \(PC\) 上に点 \(X_{1}\) をとり,実数 \(s\) を用いて
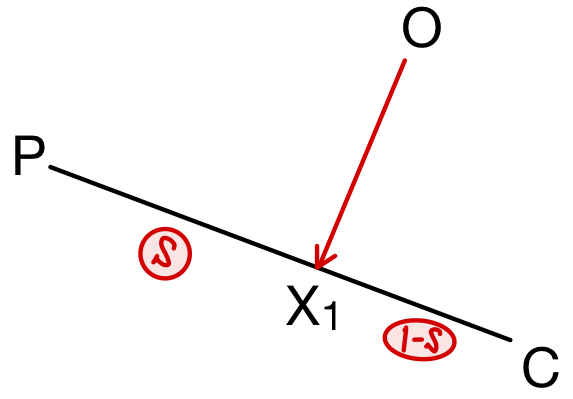
直線 \(PC\) 上に点 \(X_{1}\) をとり,実数 \(s\) を用いて
\(PX_{1}\):\(X_{1}C=s\):\(1-s\) とおくと
\(\overrightarrow{OX_{1}}=(1-s)\overrightarrow{OP}+s\overrightarrow{OC}\)
\(=\displaystyle\frac{1}{3}\overrightarrow{OA}+s\overrightarrow{OC}\) ・・・①
 また,直線 \(QR\) 上に点 \(X_{2}\) をとり,実数 \(t\) を用いて
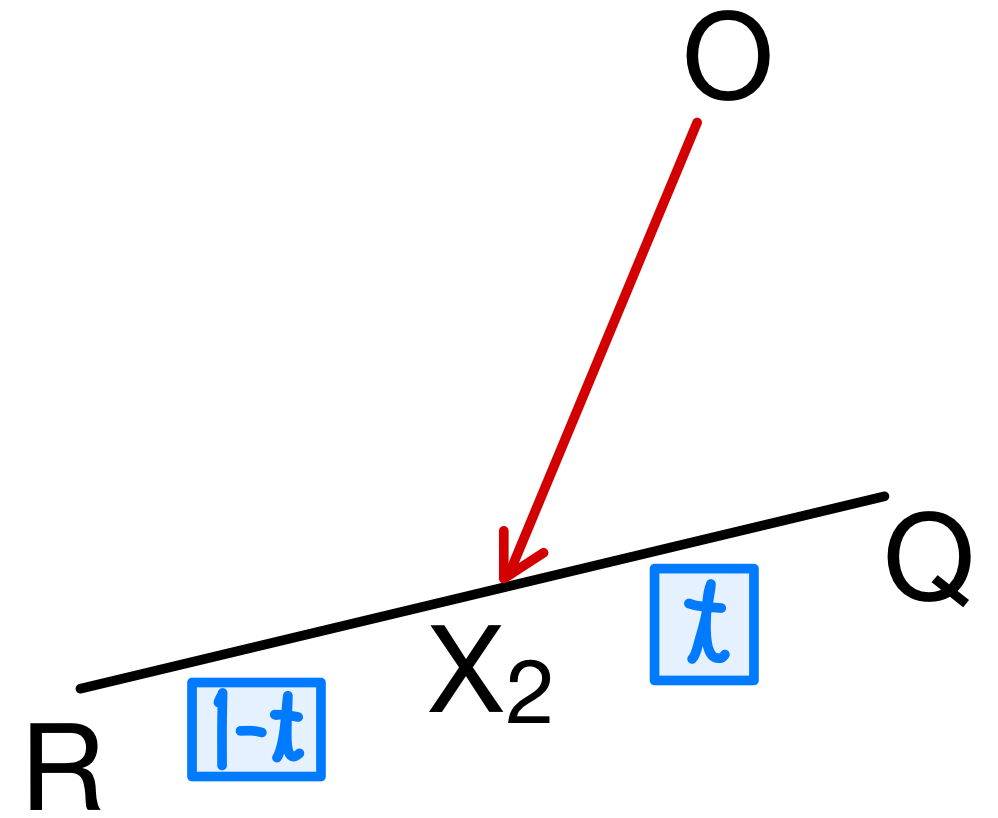
また,直線 \(QR\) 上に点 \(X_{2}\) をとり,実数 \(t\) を用いて
\(QX_{2}\):\(X_{2}R=t\):\(1-t\) とおくと
\(\overrightarrow{OX_{2}}=t\overrightarrow{OR}+(1-s)\overrightarrow{OQ}\)
ここで,点 \(R\) は 直線 \(OD\) 上より,実数 \(u\) を用いて
\(\overrightarrow{OR}=u\overrightarrow{OD}=u\overrightarrow{OA}+2u\overrightarrow{OB}+3u\overrightarrow{OC}\)
また \(\overrightarrow{OQ}=\displaystyle\frac{1}{2}\overrightarrow{OB}\) より
\(\overrightarrow{OX_{2}}=t\left(u\overrightarrow{OA}+2u\overrightarrow{OB}+3u\overrightarrow{OC}\right)+\displaystyle\frac{1}{2}(1-t)\overrightarrow{OB}\)
\(=tu\overrightarrow{OA}+\left(2tu-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{2}\right)\overrightarrow{OB}+3tu\overrightarrow{OC}\) ・・・②
直線 \(QR\) と直線 \(PC\) が交点を持つとき
\(X_{1}\) と \(X_{2}\) が一致するとき,①,②から
\(\begin{cases}\displaystyle\frac{1}{3}(1-s)=tu\\2tu-\displaystyle\frac{1}{2}t+\displaystyle\frac{1}{2}=0\\s=3tu\end{cases}\)
これを解くと,\(s=\displaystyle\frac{1}{2}\),\(t=\displaystyle\frac{5}{3}\),\(u=\displaystyle\frac{1}{10}\)
したがって,\(OR\):\(RD=u\):\(1-u=\displaystyle\frac{1}{10}\):\(\displaystyle\frac{9}{10}\)
ゆえに,\(OR\):\(RD=1\):\(9\)









コメント