【2024立命館大学(全学統一)理系】合同式、余り｜31のk乗を7，11で割った余りがともに4となるk

【2024立命館大学(全学統一2/2)・理系・第１問(２)】

解答・解説

\(mod 7\) とすると，

\(31≡3\) より

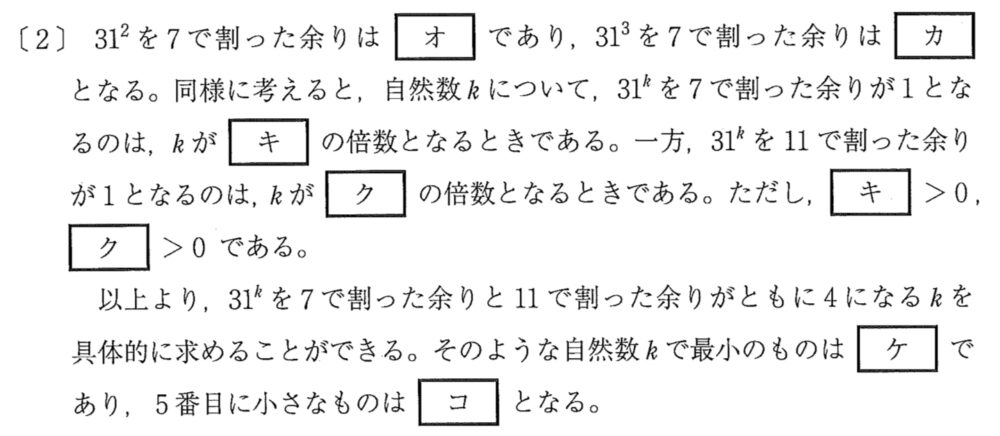
\(31^2≡3^2≡2\) ・・・［オ］

\(31^3≡3^3≡6\) ・・・［カ］

\(31^4≡3^4≡4\)

\(31^5≡3^5≡5\)

\(31^6≡3^6≡1\) より，\(31^k\) を \(7\) で割った余りが \(1\) となるのは，\(k\) が \(6\) の倍数のとき・・・［キ］

\(mod 11\) とすると，

\(31≡-2\) より

\(31^2≡(-2)^2≡4\)

\(31^3≡(-2)^3≡3\)

\(31^4≡(-2)^4≡5\)

\(31^5≡(-2)^5≡1\) より，\(31^k\) を \(11\) で割った余りが \(1\) となるのは，\(k\) が \(5\) の倍数のとき・・・［ク］

上記の結果から，

\(31^k\) を \(7\) で割った余りが \(4\) となるのは，

\(k=6x-2\) ( \(x\) は自然数 )

\(31^k\) を \(11\) で割った余りが \(4\) となるのは，

\(k=5y-3\) ( \(y\) は自然数 )　のときであるから，

\(6x-2=5y-3\) \(\iff\) \(6x-5y=-1\) ・・・①

\((x,y)=(4,5)\) は解の \(1\) つより

\(6\times4-5\times5=-1\) ・・・②

①と②の差をとると

\(6(x-4)-5(y-5)=0\)

\(6(x-4)=5(y-5)\)

\(6\) と \(5\) は互いに素であるから

整数 \(m\) を用いて \(x-4=5m\)

つまり \(x=5m+4\)

よって，\(k=6(5m+4)-2=30m+22\)

これを満たす自然数 \(k\) で最小のものは

\(m=0\) のとき \(k=22\) ・・・［ケ］

\(5\) 番目に小さいものは

\(m=4\) のとき \(k=142\) ・・・［コ］