2022京都大学・第3問(理)
\(n\) を自然数とする.
\(3\) つの整数 \(n^2+2\)、\(n^4+2\)、\(n^6+2\) の最大公約数 \(A_{n}\) を求めよ.
考え方
ユークリッド互除法
【ユークリッドの互除法】
\(2\) つの自然数 \(a\) 、\(b\) において、\(a\) を \(b\) で割ったときの商を \(q\)、余りを \(r\) とすると
\(a\) と \(b\) の最大公約数は、\(b\) と \(r\) の最大公約数に等しい

最大公約数についての問題ですから、まずはユークリッド互除法を検討しましょう!
ユークリッド互除法から
\(n^4+2=(n^2+2)(n^2-2)+6\) より、
\(n^4+2\) と \(n^2+2\) の最大公約数は、
\(n^2+2\) と \(6\) の最大公約数に等しい.
同様に、
\(n^6+2=(n^2+2)(n^4-2n^2+4)-6\) より、
\(n^6+2\) と \(n^2+2\) の最大公約数は、
\(n^2+2\) と \(6\) の最大公約数に等しい.
つまり、
\(3\) つの整数 \(n^2+2\)、\(n^4+2\)、\(n^6+2\) の最大公約数 \(A_{n}\) は、
\(n^2+2\) と \(6\) の最大公約数を求めればよい.
整数問題の極意は実験
このブログでは耳にタコができるぐらい言い続けているポイントです!
方針がつかめない場合については、とにかく実験しましょう!
具体的に実験することで、規則や法則をみつけ、答えを予想しましょう!
本問では、\(n^2+2\) と \(6\) の最大公約数を考えればよいので、
\(n = 1 , 2 , 3 , \cdots\) と具体的に代入して実験してみると、
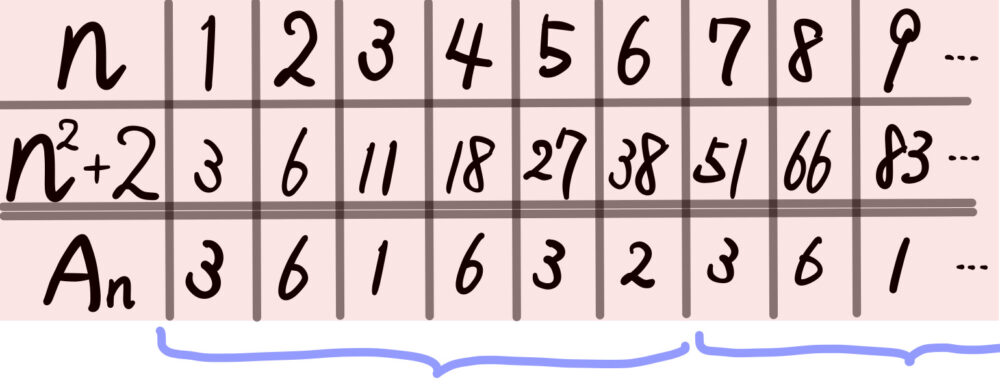
このとき、「 \(3 , 6 , 1 , 6 , 3 , 2\) 」を繰り返しそう??
周期 \(6\) で繰り返しそうであると予想することが出来る.
解答
\(n^4+2=(n^2+2)(n^2-2)+6\) 、
\(n^6+2=(n^2+2)(n^4-2n^2+4)-6\) より、
ユークリッド互除法から
\(3\) つの整数 \(n^2+2\)、\(n^4+2\)、\(n^6+2\) の最大公約数は
\(n^2+2\) と \(6\) の最大公約数に等しい.
以下では、mod 6 として考える.
(ア) \(n≡\pm1\) のとき
\(n^2+2≡3\)
よって、\(A_{n}=3\)
(イ) \(n≡\pm2\) のとき
\(n^2+2≡6≡0\)
よって、\(A_{n}=6\)
(ウ) \(n≡3\) のとき
\(n^2+2≡11≡5\)
よって、\(A_{n}=1\)
(エ) \(n≡0\) のとき
\(n^2+2≡2\)
よって、\(A_{n}=2\)
したがって、\(k\) を \(0\) 以上の整数として
\(A_{n}=\begin{cases}2 ( n=6k )\\3 ( n=6k+1 , 6k+5 )\\6 ( n=6k+2 , 6k+4 )\\1 ( n=6k+3 ) \end{cases}\)







コメント