【2023大阪大学・文系・第1問】
\(a\),\(b\) を実数とする.\(\theta\) についての方程式
\(\cos 2 \theta=a\sin \theta+b\)
が実数解をもつような点 \((a,b)\) の存在範囲を座標平面上に図示せよ.
解の配置

まず \(2\) 倍角の公式を利用することで,
\(\cos 2 \theta=a\sin \theta+b\)
\(\iff\) \(2\sin^2 \theta+a\sin \theta+b-1=0\)
ここからは \(x=\sin \theta\) と置き換えをすることで,二次関数の問題になります!

置き換えを行うので,\(x\) の範囲を考えなければいけない典型問題ですね!
\(x=\sin \theta\) と置き換えたので,\(-1≦x≦1\) で考えればOKですね!

『置き換え⇒範囲の確認』はたくさん扱っていますので,しっかりと染み付いてきましたね!
本問では,\(-1≦x≦1\) で実数解を持つかどうかを考える必要が出てきましたので・・・

解の配置!!の問題です!!!
・2次方程式が実数解を持つ
☞ 判別式Dを考える
・2次方程式が○○の範囲に実数解を持つ
☞解の配置(分離)の問題
ただ実数解を持つだけでなく、ある範囲に解を持つという問題です!

解答・解説
\(\cos 2 \theta=a\sin \theta+b\)
\(\iff\) \(2\sin^2 \theta+a\sin \theta+b-1=0\)
ここで \(x=\sin \theta\) とおくと
\(-1≦x≦1\) において
\(2x^2+ax+b-1=0\) ・・・①
ゆえに,題意は方程式①が \(-1≦x≦1\) において少なくとも \(1\) つの実数解をもつことと同値である.
したがって求める条件を以下の \(2\) つの場合で考える.
( ⅰ ) 方程式①が \(-1≦x≦1\) に \(2\) つの実数解をもつ(重解を含む)とき
( ⅱ ) 方程式①が \(-1≦x≦1\) に \(1\) つの実数解をもつ(重解を含まない)とき
( ⅰ )のとき
\(f(x)=2x^2+ax+b-1\) とすると
\(\begin{cases}f(x)=0の判別式 D≧0\\-1≦(f(x)の軸)≦1\\f(-1)≧0\\f(1)≧0 \end{cases}\)
\(\iff\) \(\begin{cases}a^2-8b+8≧0\\-1≦-\displaystyle\frac{a}{4}≦1\\a+b+1≧0\\-a+b+1≧0 \end{cases}\)
\(\iff\) \(\begin{cases}b≦\displaystyle\frac{1}{8}a^2+1\\-4≦a≦4\\b≧-a-1\\b≧a-1\end{cases}\)
( ⅱ )のとき
\(f(-1)\times f(1)≦0\)
\(\iff\) \((a+b+1)(-a+b+1)≦0\)
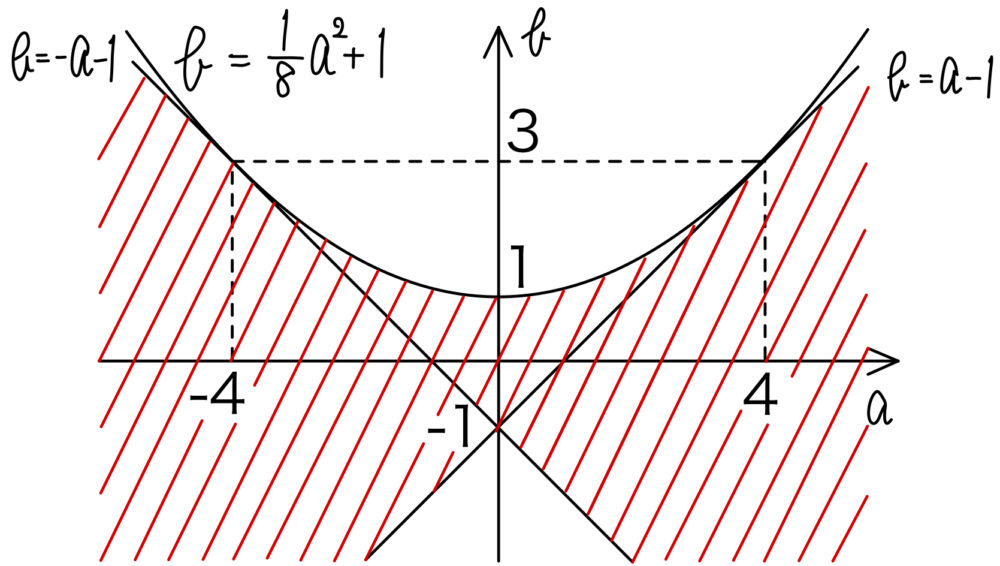
( ⅰ )( ⅱ )より,題意を満たすのは下図の斜線部分(境界を含む)








コメント