【2016神戸大学・文理(一部)】
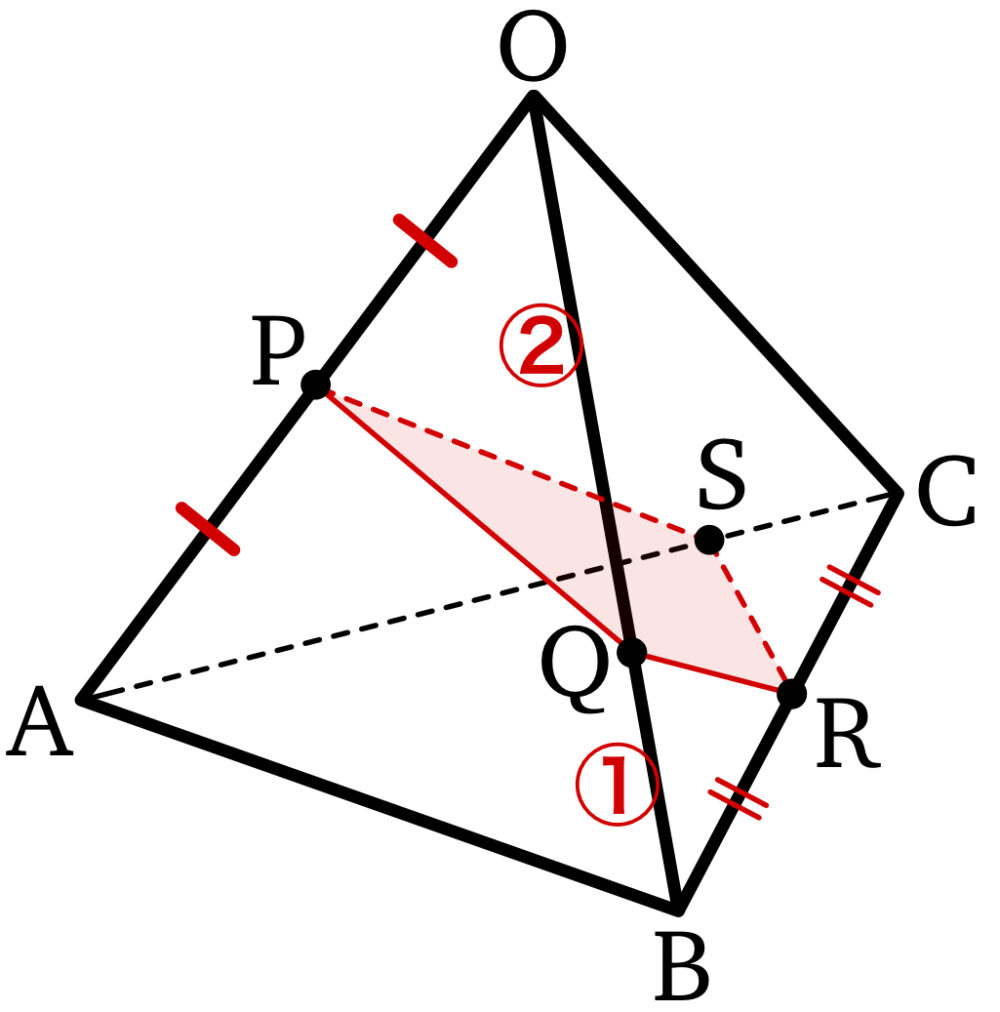
四面体 \(OABC\) において,\(P\) を辺 \(OA\) の中点,\(Q\) を辺 \(OB\) を \(2 : 1\) に内分する点,\(R\) を辺 \(BC\) の中点とする.\(P\) , \(Q\) , \(R\) を通る平面と辺 \(AC\) の交点を \(S\) とする.\(\overrightarrow{OA}=\overrightarrow{a}\) , \(\overrightarrow{OB}=\overrightarrow{b}\) ,\(\overrightarrow{OC}=\overrightarrow{c}\) とおく.以下の問に答えよ.
(1) \(\overrightarrow{PQ}\) , \(\overrightarrow{PR}\) をそれぞれ \(\overrightarrow{OA}=\overrightarrow{a}\) , \(\overrightarrow{OB}=\overrightarrow{b}\) ,\(\overrightarrow{OC}=\overrightarrow{c}\) を用いて表せ.
(2) 比 \(\left|\overrightarrow{AS}\right| : \left|\overrightarrow{SC}\right|\) を求めよ.
一次独立(空間のベクトル)
\(\overrightarrow{a}\) , \(\overrightarrow{b}\) , \(\overrightarrow{c}\) が同一平面上にないとき
\(s_{1}\overrightarrow{a}+t_{1}\overrightarrow{b}+u_{1}\overrightarrow{c}=s_{2}\overrightarrow{a}+t_{2}\overrightarrow{b}+u_{2}\overrightarrow{c}\)
\(\iff\) \(s_{1}=s_{2}\) かつ \(t_{1}=t_{2}\) かつ \(u_{1}=u_{2}\)
ベクトルで係数比較したいときは必ず一次独立なベクトルであることを必ず記述を!
方針の立て方・考え方
点 \(S\) を \(2\) 通りで表す.
① 点 \(S\) は辺 \(AC\) 上 ⇒ 共線条件
共線条件とは,異なる \(3\) 点が一直線上に並ぶときの条件
\(3\) 点 \(A\),\(B\),\(P\) が一直線上にあるとき
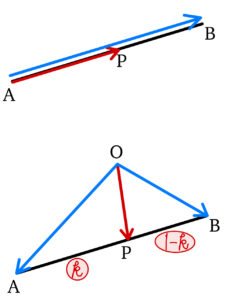 ① \(A\) を始点として考える( \(k\) は実数 )
① \(A\) を始点として考える( \(k\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}\)
② 内分の公式の利用
\(AP : PB = k : 1-k\) とするとき
\(\overrightarrow{OP}=(1-k)\overrightarrow{OA}+k\overrightarrow{OB}\)
③ ベクトル方程式
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\) かつ \(s+t=1\)
( ただし, \(s\), \(t\) は実数 )

本問では共線条件②の考え方を利用して,
\(AS : SC = t : 1-t\) とおいて考えよう!
② 点 \(S\) は平面 \(PQR\) 上 ⇒ 共面条件
共面条件とは,異なる \(4\) 点が同一平面上に並ぶときの条件
(※ \(4\) 点が同一直線状であるときは除く)
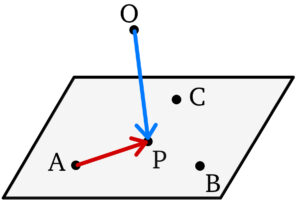 \(4\) 点 \(A\),\(B\),\(C\), \(P\) が同一平面上にあるとき
\(4\) 点 \(A\),\(B\),\(C\), \(P\) が同一平面上にあるとき
① \(A\) を始点として考える( \(k\),\(l\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}+l\overrightarrow{AC}\)
② \(O\) を始点として考える( \(s\),\(t\),\(u\) は実数 )
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)

共面条件①の考え方を利用して,
\(\overrightarrow{PS}=x\overrightarrow{PQ}+y\overrightarrow{PR}\) とおける.

解答

(1)
\(\overrightarrow{OP}=\displaystyle\frac{1}{2}\overrightarrow{a}\) , \(\overrightarrow{OQ}=\displaystyle\frac{2}{3}\overrightarrow{b}\) , \(\overrightarrow{OR}=\displaystyle\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c})\) より
\(\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}=-\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{2}{3}\overrightarrow{b}\)
\(\overrightarrow{PR}=\overrightarrow{OR}-\overrightarrow{OP}=-\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{1}{2}\overrightarrow{b}+\displaystyle\frac{1}{2}\overrightarrow{c}\)
(2)
点 \(S\) は辺 \(AC\) 上より
実数 \(t\) ( \(0≦t≦1\) ) を用いて,\(AS : SC = t : 1-t\) とおくと
\(\overrightarrow{OS}=(1-t)\overrightarrow{a}+t\overrightarrow{c}\) ・・・①
また点 \(S\) は平面 \(PQR\) 上より
実数 \(x\) , \(y\) を用いて
\(\overrightarrow{PS}=x\overrightarrow{PQ}+y\overrightarrow{PR}\) とおける.
(1)より
\(\overrightarrow{PS}=\overrightarrow{OS}-\overrightarrow{OP}=x\left(-\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{2}{3}\overrightarrow{b}\right)+y\left(-\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{1}{2}\overrightarrow{b}+\displaystyle\frac{1}{2}\overrightarrow{c}\right)\)
よって,\(\overrightarrow{OS}=\displaystyle\frac{1-x-y}{2}\overrightarrow{a}+\left(\displaystyle\frac{2}{3}x+\displaystyle\frac{y}{2}\right)\overrightarrow{b}+\displaystyle\frac{y}{2}\overrightarrow{c}\) ・・・②
\(\overrightarrow{OA}=\overrightarrow{a}\) , \(\overrightarrow{OB}=\overrightarrow{b}\) ,\(\overrightarrow{OC}=\overrightarrow{c}\) は一次独立であるから,
①,②より
\(\displaystyle\frac{1-x-y}{2}=1-t\) かつ \(\displaystyle\frac{2}{3}x+\displaystyle\frac{y}{2}=0\) かつ \(\displaystyle\frac{y}{2}=t\)
これを解くと,\(t=\displaystyle\frac{2}{3}\) , \(x=-1\) , \(y=\displaystyle\frac{4}{3}\)
したがって,\(\left|\overrightarrow{AS}\right| : \left|\overrightarrow{SC}\right|=\displaystyle\frac{2}{3} : \displaystyle\frac{1}{3}= 2 : 1\)






コメント