【問題(4STEP数B125)】
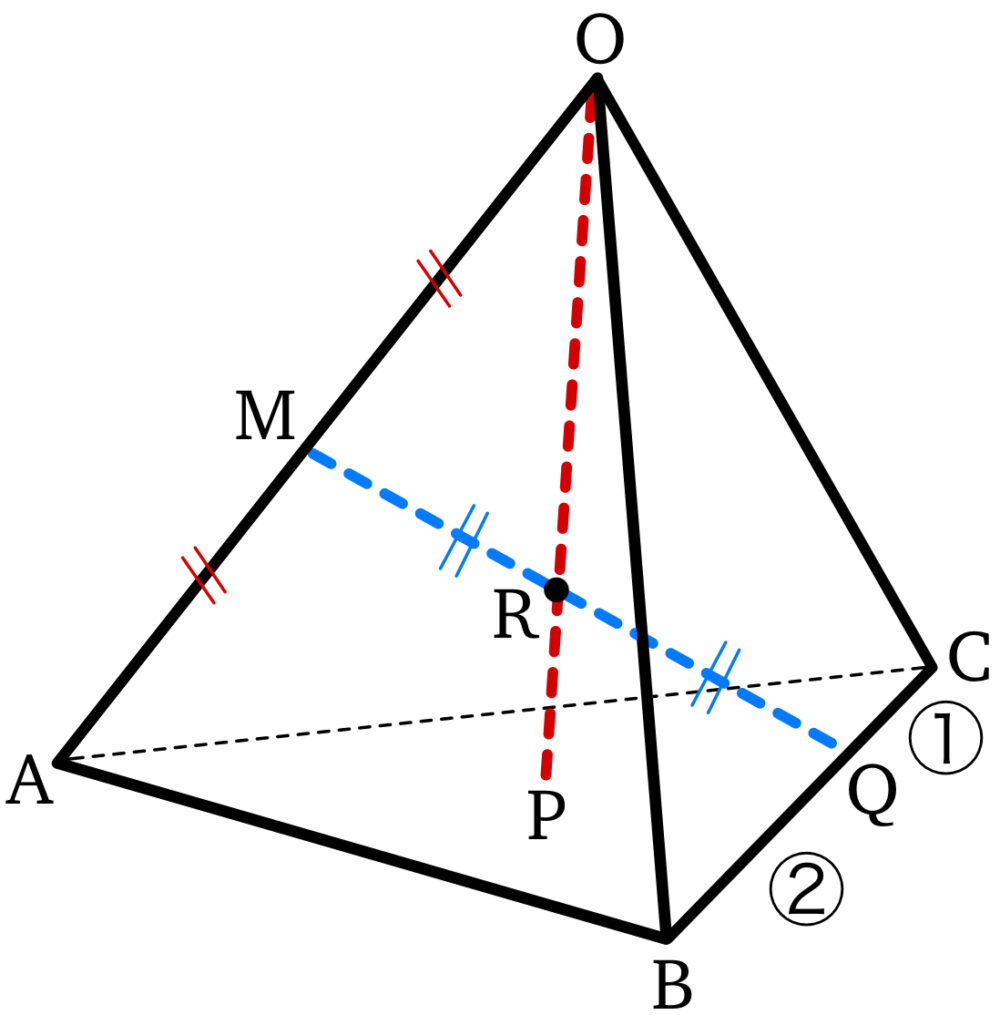
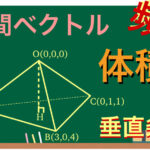
四面体 \(OABC\) の辺 \(OA\) の中点を \(M\) , 辺 \(BC\) を \(2 : 1\) に内分する点を \(Q\) , 線分 \(MQ\) の中点を \(R\) とし,直線 \(OR\) と平面 \(ABC\) の交点を \(P\) とする.\(\overrightarrow{OA}=\overrightarrow{a}\) , \(\overrightarrow{OB}=\overrightarrow{b}\) , \(\overrightarrow{OC}=\overrightarrow{c}\) とするとき,\(\overrightarrow{OP}\) を \(\overrightarrow{a}\) , \(\overrightarrow{b}\) , \(\overrightarrow{c}\) を用いて表せ.
考え方・方針の立て方
共面条件
共面条件とは,異なる \(4\) 点が同一平面上に並ぶときの条件
(※ \(4\) 点が同一直線状であるときは除く)
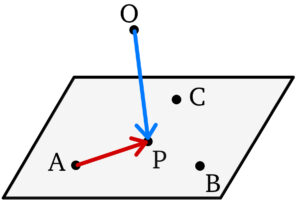 \(4\) 点 \(A\),\(B\),\(C\), \(P\) が同一平面上にあるとき
\(4\) 点 \(A\),\(B\),\(C\), \(P\) が同一平面上にあるとき
① \(A\) を始点として考える( \(k\),\(l\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}+l\overrightarrow{AC}\)
② \(O\) を始点として考える( \(s\),\(t\),\(u\) は実数 )
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)

方針の立て方について

点 \(P\) ってどんな点??
ということを2通りで考えていきましょう!

点 \(P\) は
① 直線 \(OR\) 上,② 平面 \(ABC\) 上
ということですか?

① 直線 \(OR\) 上より共線条件
② 平面 \(ABC\) 上より共面条件
が使えるってことだよ!
※ 共線条件については「【2013京都大学】1次独立と共線条件・幾何(相似)を利用した別解」を確認してください!
点 \(P\) は
① 直線 \(OR\) 上
👉 実数 \(k\) を用いて,\(\overrightarrow{OP}=k\overrightarrow{OR}\)
② 平面 \(ABC\) 上
👉 \(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)
解答
点 \(P\) は直線 \(OR\) 上より実数 \(k\) を用いて,
\(\overrightarrow{OP}=k\overrightarrow{OR}\) ・・・① とおける.
点 \(R\) は \(MQ\) の中点より,
\(\overrightarrow{OR}=\displaystyle\frac{1}{2}(\overrightarrow{OM}+\overrightarrow{OQ})\) であり,
\(\overrightarrow{OM}=\displaystyle\frac{1}{2}\overrightarrow{a}\) , \(\overrightarrow{OQ}=\displaystyle\frac{1}{3}(\overrightarrow{b}+2\overrightarrow{c})\) より,
\(\overrightarrow{OR}=\displaystyle\frac{1}{2}\left\{\displaystyle\frac{1}{2}\overrightarrow{a}+\displaystyle\frac{1}{3}(\overrightarrow{b}+2\overrightarrow{c})\right\}\)
よって,\(\overrightarrow{OR}=\displaystyle\frac{1}{4}\overrightarrow{a}+\displaystyle\frac{1}{6}\overrightarrow{b}+\displaystyle\frac{1}{3}\overrightarrow{c}\)
①より
\(\overrightarrow{OP}=\displaystyle\frac{k}{4}\overrightarrow{a}+\displaystyle\frac{k}{6}\overrightarrow{b}+\displaystyle\frac{k}{3}\overrightarrow{c}\) ・・・②
点 \(P\) は平面 \(ABC\) 上より

共面条件②の利用!
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) かつ \(s+t+u=1\)
\(\displaystyle\frac{k}{4}+\displaystyle\frac{k}{6}+\displaystyle\frac{k}{3}=1\)
よって,\(k=\displaystyle\frac{4}{3}\)
②より,\(\overrightarrow{OP}=\displaystyle\frac{1}{3}\overrightarrow{a}+\displaystyle\frac{2}{9}\overrightarrow{b}+\displaystyle\frac{4}{9}\overrightarrow{c}\)




コメント