【2008京都大学】
空間の \(1\) 点 \(O\) を通る \(4\) 直線で,どの \(3\) 直線も同一平面上にないようなものを考える.このとき,\(4\) 直線のいずれとも \(O\) 以外の点で交わる平面で,\(4\) つの交点が平行四辺形の頂点になるようなものが存在することを示せ.
考え方
一次独立・線形和
ベクトルを扱う上で最重要・基本事項の「一次独立」の考え方を利用しましょう!
空間において, \(3\) つのベクトル \(\overrightarrow{a}\) , \(\overrightarrow{b}\) , \(\overrightarrow{c}\) が \(1\) 次独立であれば,任意のベクトル \(\overrightarrow{d}\) は, \(\overrightarrow{a}\) , \(\overrightarrow{b}\) , \(\overrightarrow{c}\) の線形和となる
つまり,
\(\overrightarrow{d}=s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c}\)
を満たす実数 \(s\) , \(t\) , \(u\) が存在する.
平行四辺形であること
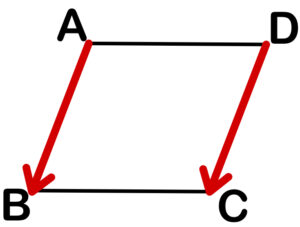
四角形 \(ABCD\) が平行四辺形
\(\iff\) \(\overrightarrow{AB}=\overrightarrow{DC}\)
解答・解説
\(4\) 直線上に,\(O\) とは異なる任意の点をそれぞれ \(A\) , \(B\) , \(C\) , \(D\) をとる.
どの \(3\) 直線も同一平面上にないので,\(\overrightarrow{OA}\) , \(\overrightarrow{OB}\) , \(\overrightarrow{OC}\) は \(1\) 次独立である.
よって,
\(\overrightarrow{OD}=s\overrightarrow{OA}+t\overrightarrow{OB}+u\overrightarrow{OC}\) ・・・①
を満たす実数 \(s\) , \(t\) , \(u\) が存在する.
ここで,\(s=0\) と仮定すると①より
\(\overrightarrow{OD}=t\overrightarrow{OB}+u\overrightarrow{OC}\) となり,これは点 \(D\) が平面 \(OBC\) 上にあることになるため条件に反する.したがって,\(s\not=0\)
同様に考え,\(s\not=0\) , \(t\not=0\) , \(u\not=0\) ・・・②
このとき,①より
\(\overrightarrow{OD}-u\overrightarrow{OC}=s\overrightarrow{OA}+t\overrightarrow{OB}\)
\(\iff\) \(\overrightarrow{OD}-u\overrightarrow{OC}=s\overrightarrow{OA}-\left(-t\overrightarrow{OB}\right)\) であるから
\(\overrightarrow{OP}=s\overrightarrow{OA}\) , \(\overrightarrow{OQ}=-t\overrightarrow{OB}\) , \(\overrightarrow{OR}=u\overrightarrow{OC}\) とおくと
\(\overrightarrow{OD}-\overrightarrow{OR}=\overrightarrow{OP}-\overrightarrow{OQ}\)
つまり,\(\overrightarrow{RD}=\overrightarrow{QP}\)
②より,\(4\) 点 \(P\) , \(Q\) , \(R\) , \(D\) は異なる点であり,\(3\) 点 \(P\) , \(Q\) , \(R\) は同一直線上にない.
したがって,四角形 \(PQRD\) は平行四辺形である.
以上より題意は示された.







コメント