【2021 北海道大学・理,工(後期)】
(1) 整数 \(m\) に対して,\(m^2\) を \(4\) で割った余りは \(0\) または \(1\) であることを示せ.
(2) 自然数 \(n\)、\(k\) が \(25\times3^n=k^2+176\) ・・・ (※) を満たすとき、\(n\) は偶数であることを示せ.
(3) (2)の関係式(※)を満たす自然数の組 \(( n , k )\) をすべて求めよ.
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
この3つのPointは絶対に頭の中に叩き込んでください!
☆平方数・指数はmod 3,mod 4 が有効
難関大学ではよく出題されるPointの1つ!
まずは下の表を見てください。
平方数において
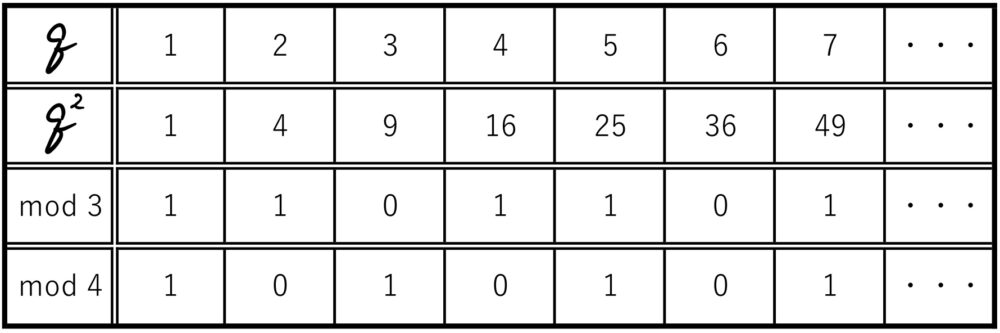
何かの2乗(平方数)において、
mod 3→「1,1,0」の繰り返し
mod 4→「1,0」の繰り返し
という規則が存在!
指数に関しても、同様に考えると規則を持つことが確認できる。
詳しくは類題として「2021 兵庫県立大学【整数】平方数には合同式(mod)を使え!」を参考にしてください。
また、合同式をまだ学習していない、または不安と言う人は、
で合同式をマスターしよう!
整数問題において、合同式が使えないのは致命的です・・・。
参考:平方数とmod 3、4、5、8について
上で紹介したように、平方数と合同式は非常に相性抜群です!
特に \(mod 3\) や \(mod 4\) は頻出ですので絶対に抑え、さらに参考として、\(mod 5\)、\(mod 8\) についても 紹介しておきます。
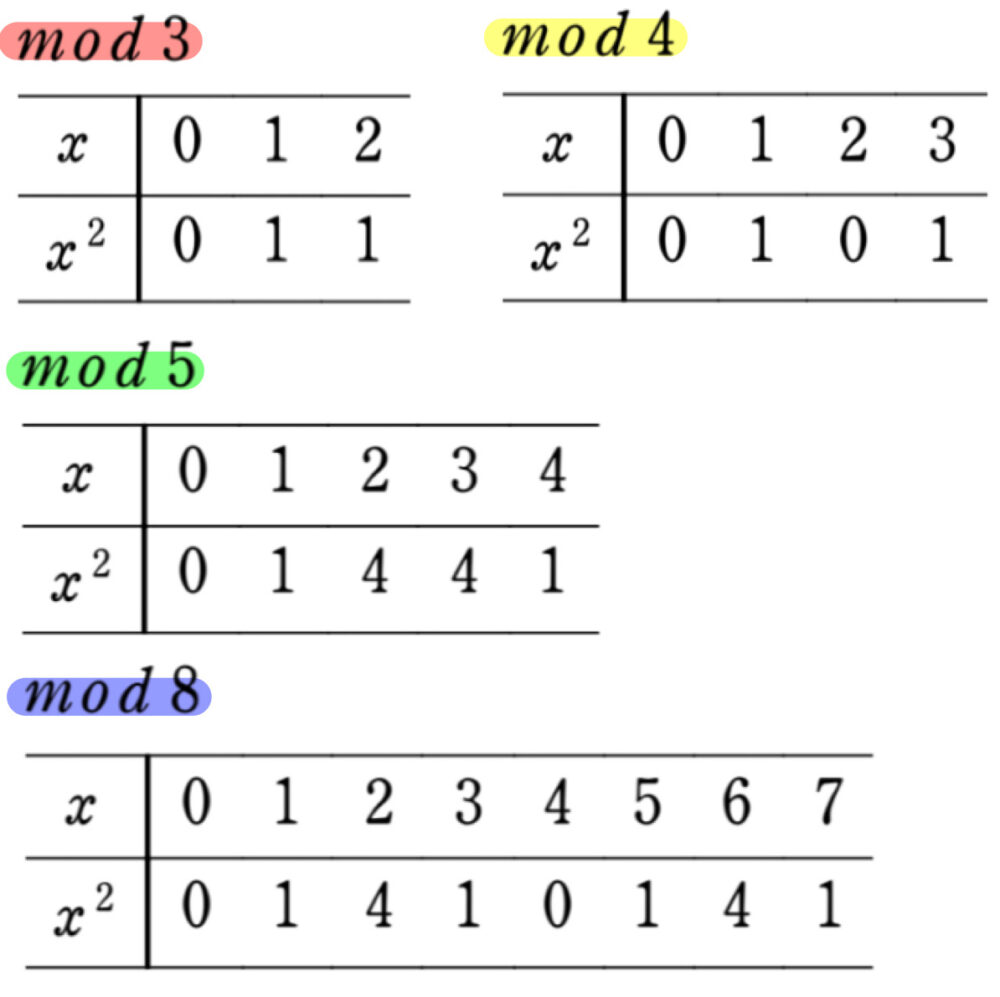
- mod 3 ➡ 「0、1」のみ
- mod 4 ➡ 「0、1」のみ
- mod 5 ➡ 「0、1、4」のみ
- mod 8 ➡ 「0、1、4」のみ
解答
【2021 北海道大学・理,工(後期)】
(1) 整数 \(m\) に対して,\(m^2\) を \(4\) で割った余りは \(0\) または \(1\) であることを示せ.
(2) 自然数 \(n\)、\(k\) が \(25\times3^n=k^2+176\) ・・・ (※) を満たすとき、\(n\) は偶数であることを示せ.
(3) (2)の関係式(※)を満たす自然数の組 \(( n , k )\) をすべて求めよ.
(1) 解答
以下、法を \(4\) として考える.
・ \(m ≡ 0\) のとき \(m^2 ≡ 0\)
・ \(m ≡ 1\) のとき \(m^2 ≡ 1\)
・ \(m ≡ 2\) のとき \(m^2 ≡ 4 ≡ 0\)
・ \(m ≡ 3\) のとき \(m^2 ≡ 9 ≡ 1\)
以上より、整数 \(m\) に対して,\(m^2\) を \(4\) で割った余りは \(0\) または \(1\) である.
(2) 解答
背理法で考える.
つまり、自然数 \(n\)、\(k\) が \(25\times3^n=k^2+176\) ・・・ (※) を満たすとき、
\(n\) は奇数であると仮定する.
このとき、法を \(4\) として考えると
\(3 ≡ -1\) より、 \(3^n ≡ (-1)^n\)
\(n\) は奇数であるから、
\(3^n ≡ -1 ≡ 3\)
また、\(25 ≡ 1\) 、\(176 ≡ 0\) 、
以上より、
(左辺) \(=25\times3^n ≡ 1\times3 = 3\)
(右辺) \(=k^2+176 ≡ k^2\)
(1)の結果から \(k^2 ≡ 0\) または \(1\) であるから、
(右辺)\( ≡ 0\) または \(1\)
よって両辺を \(4\) で割った余りが一致しないため、矛盾.
したがって、自然数 \(n\)、\(k\) が \(25\times3^n=k^2+176\) ・・・ (※) を満たすとき、\(n\) は偶数である.
(3) 解答
(2)より、\(n=2x\) (\(x\) は自然数) とおける.
(※)より
\(25\times3^{2x}=k^2+176\)








コメント