【2021数学ⅡB(第2日程)：第５問ベクトル】

(１)問題と解答・解説《ア〜サ》

(１)解答・解説《ア〜サ》

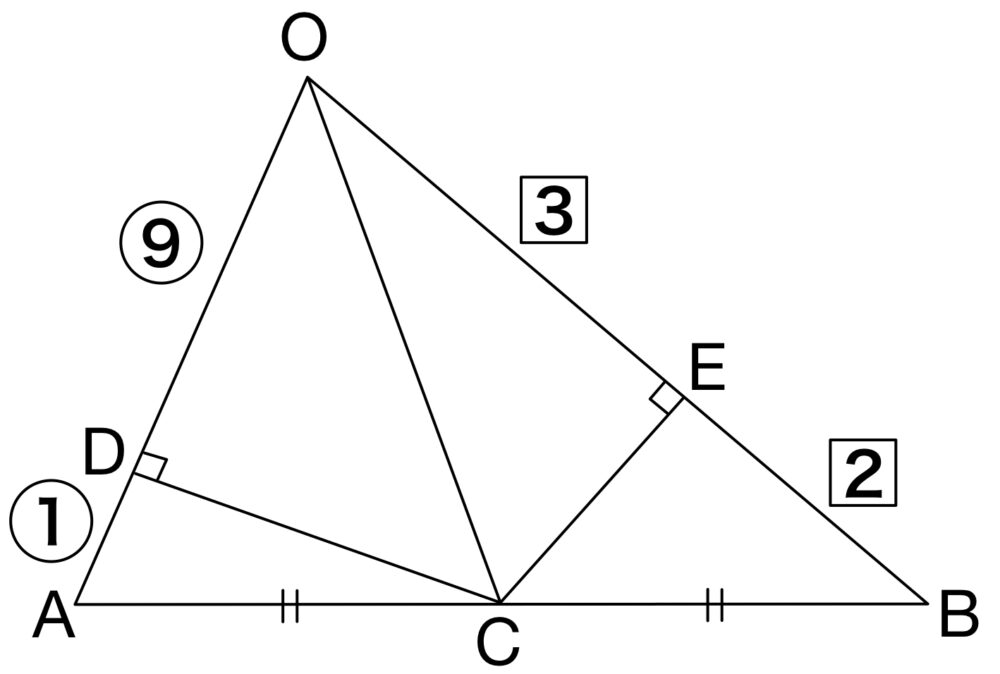
\(\left|\overrightarrow{OA}\right|^2=(-1)^2+2^2+0^2=5\) ・・・《ア》

また，\(\overrightarrow{OD}=\displaystyle\frac{9}{10}\overrightarrow{OA}\) ・・・《イ〜エ》 であることにより，

\(\overrightarrow{CD}=\overrightarrow{OD}-\overrightarrow{OC}=\displaystyle\frac{9}{10}\overrightarrow{OA}-\displaystyle\frac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\)

よって，\(\overrightarrow{CD}=\displaystyle\frac{2}{5}\overrightarrow{OA}-\displaystyle\frac{1}{2}\overrightarrow{OB}\) ・・・《オ〜ク》

\(\overrightarrow{OA}\perp\overrightarrow{CD}\) から \(\overrightarrow{OA}\cdot\overrightarrow{CD}=0\)

\(\overrightarrow{OA}\cdot\left(\displaystyle\frac{2}{5}\overrightarrow{OA}-\displaystyle\frac{1}{2}\overrightarrow{OB}\right)=0\)

\(\displaystyle\frac{2}{5}\left|\overrightarrow{OA}\right|^2-\displaystyle\frac{1}{2}\overrightarrow{OA}\cdot\overrightarrow{OB}=0\)

\(\displaystyle\frac{2}{5}\times 5-\displaystyle\frac{1}{2}\overrightarrow{OA}\cdot\overrightarrow{OB}=0\)

よって，\(\overrightarrow{OA}\cdot\overrightarrow{OB}=4\) ・・・《ケ》

これにより，\(\overrightarrow{OA}\cdot\overrightarrow{OB}=-2+2p=4\)

ゆえに，\(p=3\)

また，\(\overrightarrow{CE}=\overrightarrow{OE}-\overrightarrow{OC}=\displaystyle\frac{3}{5}\overrightarrow{OB}-\displaystyle\frac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\)

よって，\(\overrightarrow{CE}=-\displaystyle\frac{1}{2}\overrightarrow{OA}+\displaystyle\frac{1}{10}\overrightarrow{OB}\) であり

\(\overrightarrow{OB}\perp\overrightarrow{CE}\) から \(\overrightarrow{OB}\cdot\overrightarrow{CE}=0\)

\(\overrightarrow{OB}\cdot\left(-\displaystyle\frac{1}{2}\overrightarrow{OA}+\displaystyle\frac{1}{10}\overrightarrow{OB}\right)=0\)

\(-\displaystyle\frac{1}{2}\overrightarrow{OA}\cdot\overrightarrow{OB}+\displaystyle\frac{1}{10}\left|\overrightarrow{OB}\right|^2=0\)

\(-\displaystyle\frac{1}{2}\times 4+\displaystyle\frac{1}{10}\left|\overrightarrow{OB}\right|^2=0\)

\(\left|\overrightarrow{OB}\right|^2=20\) であるから

\(\left|\overrightarrow{OB}\right|^2=2^2+p^2+q^2=20\)

\(p=3\) より，\(q^2=7\)

\(q>0\) より，\(q=\sqrt{7}\)

したがって，\(B(2,3,\sqrt{7})\) ・・・《コサ》

(２)問題と解答・解説《シ〜ツ》

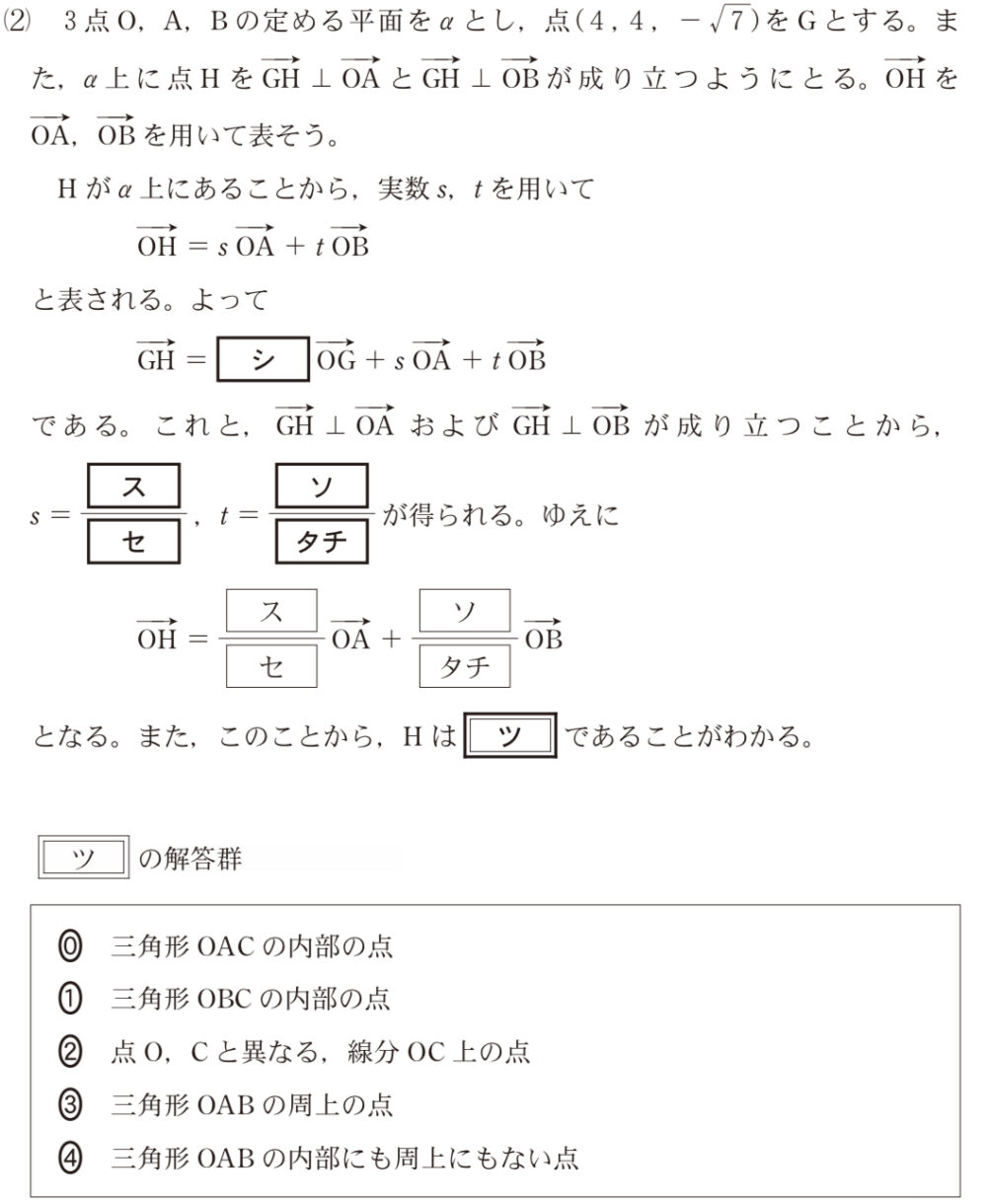
(２)解答・解説《シ〜ツ》

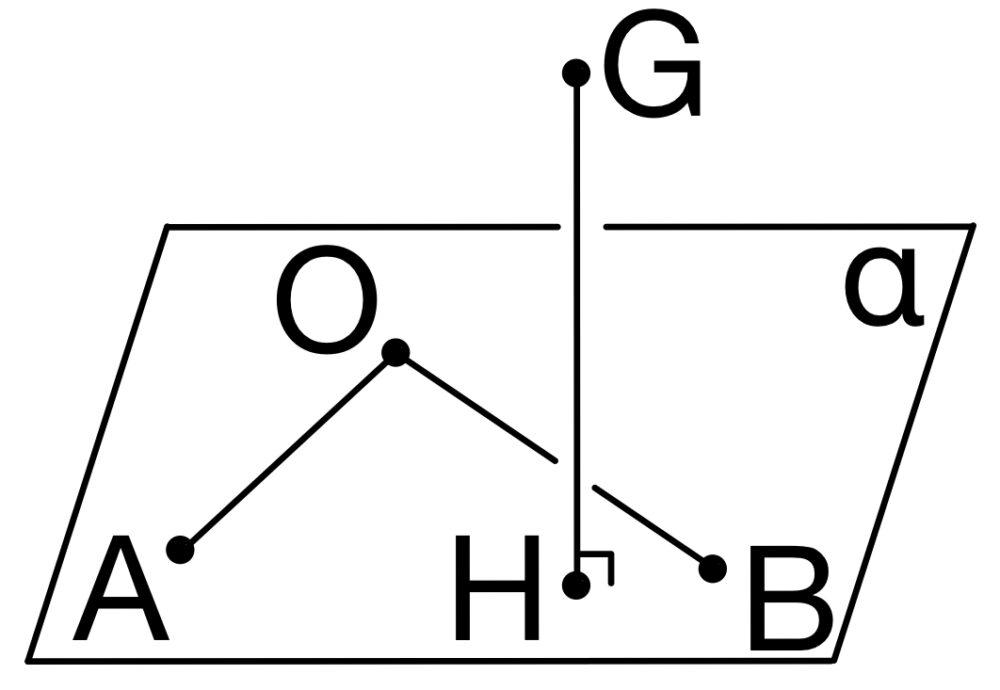
点 \(H\) は \(\alpha\) 上より，実数 \(s\)，\(t\) を用いて

\(\overrightarrow{OH}=s\overrightarrow{OA}+t\overrightarrow{OB}\) と表される．

\(\overrightarrow{GH}=\overrightarrow{OH}-\overrightarrow{OG}\) より

\(\overrightarrow{GH}=-\overrightarrow{OG}+s\overrightarrow{OA}+t\overrightarrow{OB}\) ・・・《シ》

\(\overrightarrow{GH}=(-s,2s,0)+(2t,3t,\sqrt{7}t)-(4,4,-\sqrt{7})\)

\(=(-s+2t-4,2s+3t-4,\sqrt{7}t+\sqrt{7})\)

\(\overrightarrow{GH}\perp\overrightarrow{OA}\) および \(\overrightarrow{GH}\perp\overrightarrow{OB}\) より

\(\overrightarrow{GH}\cdot\overrightarrow{OA}=0\) かつ \(\overrightarrow{GH}\cdot\overrightarrow{OB}=0\)

\(\overrightarrow{GH}\cdot\overrightarrow{OA}=0\) のとき

\(-(-s+2t-4)+2(2s+3t-4)+0\cdot(\sqrt{7}t+\sqrt{7})=0\)

よって，\(5s+4t-4=0\) ・・・①

\(\overrightarrow{GH}\cdot\overrightarrow{OB}=0\) のとき

\(2(-s+2t-4)+3(2s+3t-4)+\sqrt{7}(\sqrt{7}t+\sqrt{7})=0\)

よって，\(4s+20t-13=0\) ・・・②

①，②より，\(s=\displaystyle\frac{1}{3}\) ，\(t=\displaystyle\frac{7}{12}\) ・・・《ス〜チ》

ゆえに，\(\overrightarrow{OH}=\displaystyle\frac{1}{3}\overrightarrow{OA}+\displaystyle\frac{7}{12}\overrightarrow{OB}\)

これより，\(\overrightarrow{OH}=\displaystyle\frac{11}{12}\left(\displaystyle\frac{4}{11}\overrightarrow{OA}+\displaystyle\frac{7}{11}\overrightarrow{OB}\right)\) より

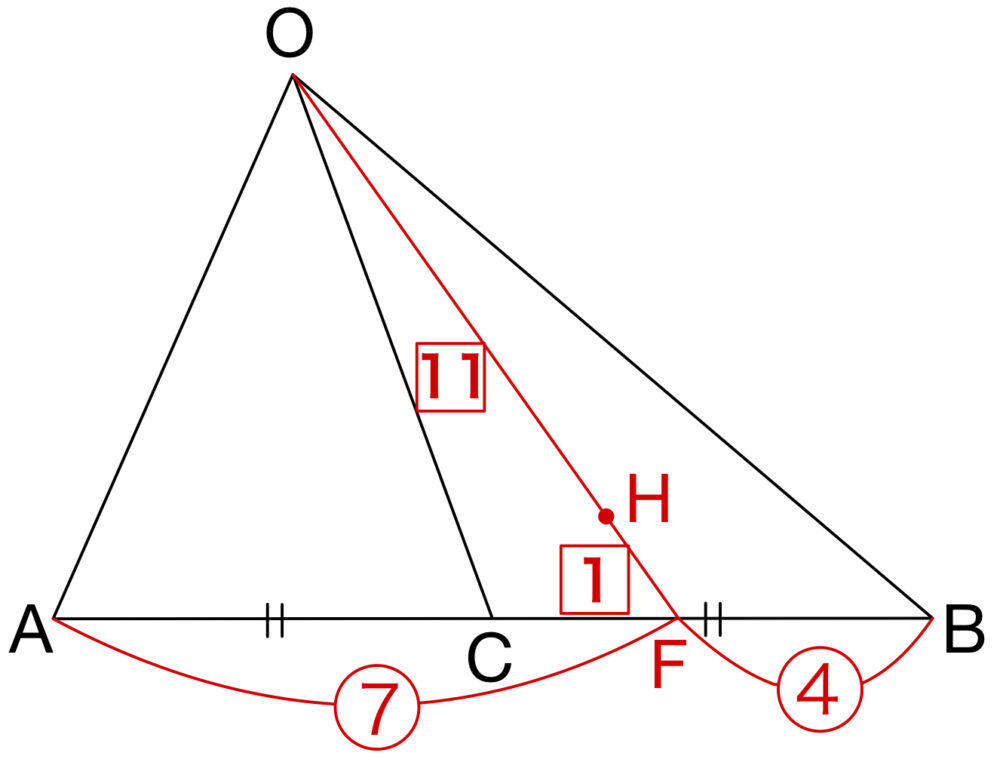線分 \(AB\) を \(7：4\) に内分する点を \(F\) とすると，\(\overrightarrow{OH}=\displaystyle\frac{11}{12}\overrightarrow{OF}\) であるから，

点 \(H\) は線分 \(OF\) を \(11：1\) に内分する点である．

したがって点 \(H\) は，①三角形 \(OBC\) の内部の点・・・《ツ》