極と極線｜円外の点から円に引いた接線の2接点を通る直線

\(xy\) 平面上に円 \(C\) : \(x^2+y^2=1\) がある．

円 \(C\) の外部の点 \(P(a,b)\) から \(C\) に引いた \(2\) 本の接線の接点を \(Q\) , \(R\) とする．

直線 \(QR\) の方程式を求めよ．

円に関する極と極線

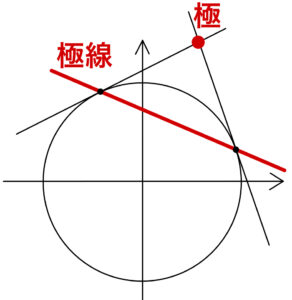円外の点 \(P(a,b)\) から

円 \(x^2+y^2=r^2\) に引いた接線の \(2\) 接線を通る直線は，

\(x_{1}x+y_{1}y=r^2\) ・・・①

※ 点 \(P\) を円に関する極，直線①を円に関する極線という．

円に関する極と極線と言います！

本文はこの性質を証明する問題になります！

有名な問題ですので，まずは結果を覚えておきましょう！

円 \(C\) : \(x^2+y^2=r^2\) 上の点 \((x_{0},y_{0})\) における接線の方程式は

\(x_{0}x+y_{0}y=r^2\)

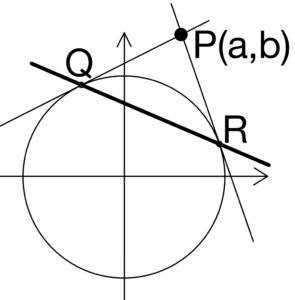\(Q(x_{1},y_{1})\) , \(R(x_{2},y_{2})\) とおく．

\(Q\) , \(R\) における円 \(C\) の接線の方程式はそれぞれ

\(x_{1}x+y_{1}y=1\)

\(x_{2}x+y_{2}y=1\)

これらはともに \(P(a,b)\) を通るので

\(ax_{1}+by_{1}=1\)

\(ax_{2}+by_{2}=1\)

これは，直線 \(ax+by=1\) が \(2\) 点 \(Q\) , \(R\) を通ることを示している．

\(2\) 点 \(Q\) , \(R\) を通る直線はただ \(1\) つであるから，

したがって求める直線の方程式は \(ax+by=1\)