減衰曲線の極値、x＝aで極値をもつ(必要条件)、無限等比数列の収束と和

（１）考え方・解答・解説

(１)\(x=a\) で極値をもつとき(逆の確認を！)

必要条件で考え、十分条件の確認をしっかりしましょう！

(１)解答・解説

\(f^{\prime}(x)=ae^{ax}\sin x+e^{ax}\cos x\)

\(=e^{ax}(a\sin x+\cos x)\)

\(x=\displaystyle\frac{\pi}{4}\) で極大値をとるとき，

\(f^{\prime}\left(\displaystyle\frac{\pi}{4}\right)=e^{\frac{\pi a}{4}}\cdot\displaystyle\frac{a+1}{\sqrt{2}}=0\)

よって，\(a=-1\)

このとき，\(f(x)=e^{-x}\sin x\)

\(f^{\prime}(x)=e^{-x}(-\sin x+\cos x)\)

\(=-\sqrt{2}e^{-x}\sin\left(x-\displaystyle\frac{\pi}{4}\right)\) ・・・①

となるので，\(f^{\prime}(x)\) の符号は \(x=\displaystyle\frac{\pi}{4}\) の前後で正から負に変化するため， \(x=\displaystyle\frac{\pi}{4}\) で極大値をとる．

したがって，\(a=-1\)

(２)考え方・解答・解説

(２)減衰曲線

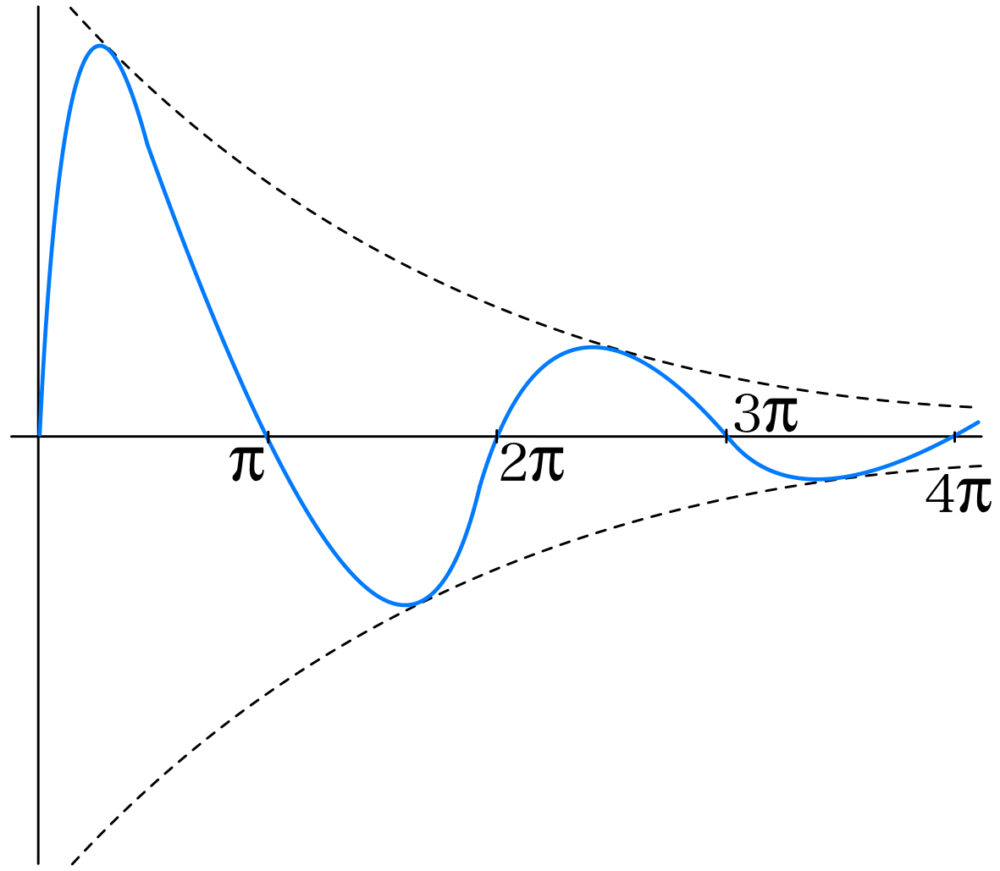
\(y=e^{-x}\sin x\) のグラフは，振幅が小さくなっていき，非常に早く \(0\) に近づく．このような曲線を減衰曲線と言います。

グラフの概形は有名ですから覚えておきましょう！

\(f(x)\) の極大値は，公比が \(e^{-2\pi}\) の無限等比数列となります。収束条件を確認した上で，無限等比数列の和を考えましょう！

無限等比数列の収束条件、和について確認は

【無限等比級数】収束条件と和｜Σ(cosx-sinx)^k

を参考に！！

(２)解答・解説

\(f^{\prime}(x)=-\sqrt{2}e^{-x}\sin\left(x-\displaystyle\frac{\pi}{4}\right)\) ・・・①

①より，\(x>0\) で極大となるのは

\(x-\displaystyle\frac{\pi}{4}=2n\pi\) ( \(n\) は \(0\) 以上の整数 ) のとき

よって極大値は，

\(f\left(\displaystyle\frac{\pi}{4}+2n\pi\right)=e^{-\left(\frac{\pi}{4}+2n\pi\right)}\cdot\displaystyle\frac{1}{\sqrt{2}}=\displaystyle\frac{e^{-\frac{\pi}{4}}}{\sqrt{2}}\left(e^{-2\pi}\right)^n\)

となり，これらの総和は，公比が \(e^{-2\pi}\) の無限等比級数となる．

\(-1<e^{-2\pi}<1\) より，和は収束し，その和は

\(\displaystyle\frac{e^{-\frac{\pi}{4}}}{\sqrt{2}(1-e^{-2\pi})}\)