【2021数学ⅡB(第2日程)】第4問(数列)
(1)問題と解答・解説《ア〜オ》

(1)解答・解説《ア〜オ》
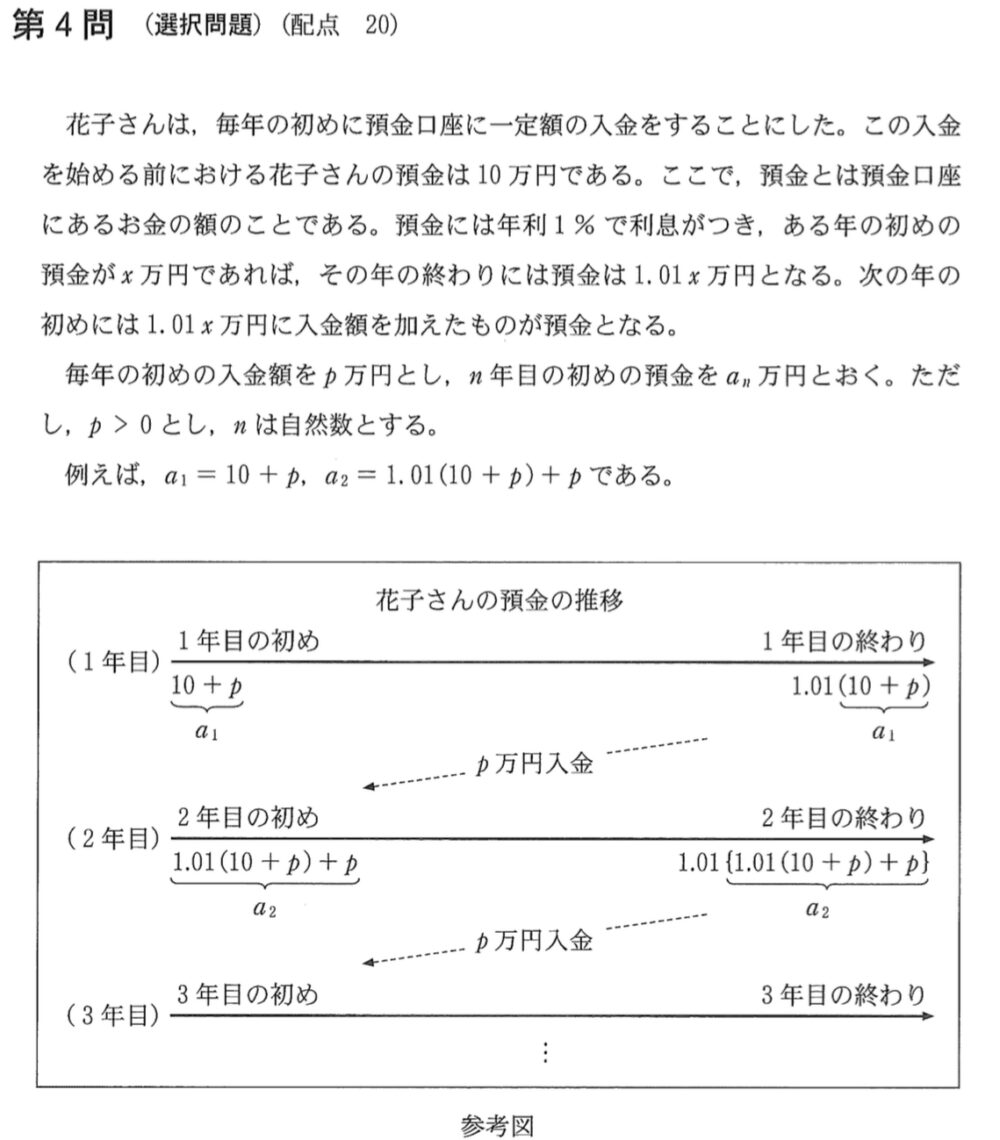
\(n\) 年目の初めの預金が \(a_{n}\) 万円のとき,
\(n\) 年目の終わりの預金は \(1.01\times a_{n}\) 万円となる.
よって \(n+1\) 年目の初めの預金は, \(a_{n}+p\) 万円であるから,
\(a_{3}=1.01\times a_{2}+p=\)\(1.01\left\{1.01(10+p)+p\right\}+p\) ・・・《ア:②》
が成り立ち,また,
\(a_{n+1}=1.01a_{n}+p\) ・・・《イ:⓪,ウ:③》

二項間の特性方程式型の頻出形態!!
あとは特性方程式を解いてあげればOKですね!
漸化式に不安がある人は必ず,
は最低でも確認しておくように!
\(a_{n+1}=1.01a_{n}+p\) ・・・①
\(\alpha=1.01\alpha+p\) ・・・②
② \(\iff\) \(\alpha=-100p\)
①と②の差をとると
\(a_{n+1}-\alpha=1.01(a_{n}-\alpha)\)
よって,\(a_{n+1}+100p=1.01(a_{n}+100p)\) ・・・《エ:④,オ:⓪》
と変形でき,\(a_{n}\) を求めることができる.
(1)問題と解答・解説《カ〜ケ》

(1)解答・解説《カ〜ケ》
・\(1\) 年目の初めに入金した \(p\) 万円は,
\(n\) 年目の初めには \(p\times 1.01^{n-1}\) 万円・・・《カ:②》
・\(2\) 年目の初めに入金した \(p\) 万円は,
\(n\) 年目の初めには \(p\times 1.01^{n-2}\) 万円・・・《カ:③》
・・・
・\(n\) 年目の初めに入金した \(p\) 万円は,
\(n\) 年目の初めには \(p\) 万円のままである.
これより
\(a_{n}=10\times 1.01^{n-1}+p\times 1.01^{n-1}+p\times 1.01^{n-2}+\cdots+p\)
\(=10\times 1.01^{n-1}+p\displaystyle\sum_{k=1}^{n}{1.01^{k-1}}\) ・・・《ク:②》
となることがわかる.
ここで,\(\displaystyle\sum_{k=1}^{n}{1.01^{k-1}}\) は初項が \(1\),公比が \(1.01\),項数 \(n\) の等比数列の和であるから
\(\displaystyle\sum_{k=1}^{n}{1.01^{k-1}}=\displaystyle\frac{1.01^n-1}{1.01-1}=\)\(100(1.01^n-1)\) ・・・《ケ:①》
(2)問題と解答・解説《コ〜セ》

(2)解答・解説《コ〜セ》
\(10\) 年目の終わりの預金は \(1.01a_{10}\) 万円・・・《コ:③》
(1)の結果から,\(r=1.01\) とおくと
\(a_{n}=10r^{n-1}+100p(r^n-1)\) なので
\(a_{10}=10r^{9}+100p(r^{10}-1)\)
よって,\(1.01a_{10}≧30\)
\(\iff\) \(10r^{10}+101p(r^{10}-1)≧30\)
\(\iff\) \(101p(r^{10}-1)≧30-10r^{10}\)
\(\iff\) \(p≧\displaystyle\frac{30-10r^{10}}{101(r^{10}-1)}\) ・・・《サ〜セ》
(3)問題と解答・解説《ソ》

(3)解答・解説《ソ》
\(r=1.01\) とおく.\(a_{n}=10r^{n-1}+100p(r^n-1)\) であり,
(1)と同様に考えていくと
\(1\) 年目の入金を始める前に \(13\) 万円の預金がある場合,
\(n\) 年目の初めの預金を \(b_{n}\) 万円とすると
\(b_{n}=13r^{n-1}+100p(r^n-1)\)
これらの差を考えると
\(b_{n}-a_{n}=3r^{n-1}=\)\(3\times 1.01^{n-1}\) ・・・《ソ:⑧》







コメント