【2023大阪公立大学・理系・第2問】
\(i\) は虚数単位を表すものとする.複素数 \(z\) に関する方程式
\(z=\left(\cos\displaystyle\frac{\pi}{3}-i\sin\displaystyle\frac{\pi}{3}\right)\overline{z}\)
の表す複素数平面上の図形を \(l\) とする.次の問いに答えよ.
問1 \(l\) は直線であることを証明せよ.
問2 直線 \(l\) に関して複素数 \(w\) と対称な点を \(w\) の式で表せ.
問3 複素数 \(z\) に対して,\(z\) を点 \(1\) を中心に反時計回りに \(\displaystyle\frac{2\pi}{3}\) 回転した点を \(z_{1}\) とし,次に \(z_{1}\) を原点を中心に反時計回りに \(\displaystyle\frac{2\pi}{3}\) 回転した点を \(z_{2}\) とする.さらに,直線 \(l\) に関して \(z_{2}\) と対称な点を \(f(z)\) とする.\(f(z)\) を \(z\) の式で表せ.
問4 \(f(z)\) は問3のとおりとする.複素数 \(z\) に関する方程式
\(f(z)=-z-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
の表す複素数平面上の図形を図示せよ.
解答・解説
問1
\(x\),\(y\) を実数として \(z=x+yi\) とおくと
\(\overline{z}=x-yi\) より
\(x+yi=\left(\cos\displaystyle\frac{\pi}{3}-i\sin\displaystyle\frac{\pi}{3}\right)(x-yi)\)
\(\iff\) \(x+yi=\left(\displaystyle\frac{1}{2}x-\displaystyle\frac{\sqrt{3}}{2}y\right)+\left(-\displaystyle\frac{\sqrt{3}}{2}x-\displaystyle\frac{1}{2}y\right)i\)
よって
\(\begin{cases}x=\displaystyle\frac{1}{2}x-\displaystyle\frac{\sqrt{3}}{2}y\\y=-\displaystyle\frac{\sqrt{3}}{2}x-\displaystyle\frac{1}{2}y\end{cases}\)
\(\iff\) \(y=-\displaystyle\frac{\sqrt{3}}{3}x\) となり \(l\) は直線である.
問2 原点を通る直線に関する対称点
\(\alpha\) ( \(\alpha\not=0\) ) 、\(\beta\)、\(\gamma\) は複素数とする.複素平面上で、\(\beta\)、\(\gamma\) とが、\(O\) と \(\alpha\) とを通る直線に関して対称な点であるためには、
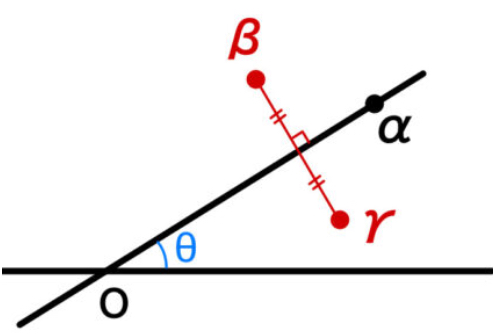 「\(\overline{\alpha}\gamma=\alpha\overline{\beta}\)」
「\(\overline{\alpha}\gamma=\alpha\overline{\beta}\)」
が必要十分条件となる.

原点を通る直線に関する対称な点については頻出!
しっかり証明できるように!ここでは証明については省略します。
証明は「【数Ⅲ】複素数平面まとめ⑥(原点を通る直線に関する対称点)|入試問題演習」を参考に!

問1より直線 \(l\):\(y=-\displaystyle\frac{\sqrt{3}}{3}x\)
\(-\displaystyle\frac{\sqrt{3}}{3}=\tan\displaystyle\frac{5\pi}{6}\) で,
\(\alpha=\cos\displaystyle\frac{5\pi}{6}+i\sin\displaystyle\frac{5\pi}{6}\) とおく.
直線 \(l\) に関して複素数 \(w\) と対称な点を \(w^{\prime}\) とすると
\(\overline{\alpha}w^{\prime}=\alpha\overline{w}\) を満たす.
両辺に \(\alpha\) をかけると
\(\alpha\overline{\alpha}w^{\prime}=\alpha^2\overline{w}\)
\(\alpha\overline{\alpha}=|\alpha|^2=1\) より
\(w=\alpha^2\overline{w}=\left(\cos\displaystyle\frac{5\pi}{6}+i\sin\displaystyle\frac{5\pi}{6}\right)^2\overline{w}\)
\(w=\left(\cos\displaystyle\frac{5\pi}{3}+i\sin\displaystyle\frac{5\pi}{3}\right)\overline{w}=\left(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{w}\)
問3 一般の点を中心とする回転移動
点 \(\alpha\) を中心に、点 \(\beta\) を \(k\) 倍して、角 \(\theta\) だけ回転した点が \(\gamma\) のとき
\(\gamma-\alpha=k(\cos \theta+i \sin \theta) (\beta-\alpha)\)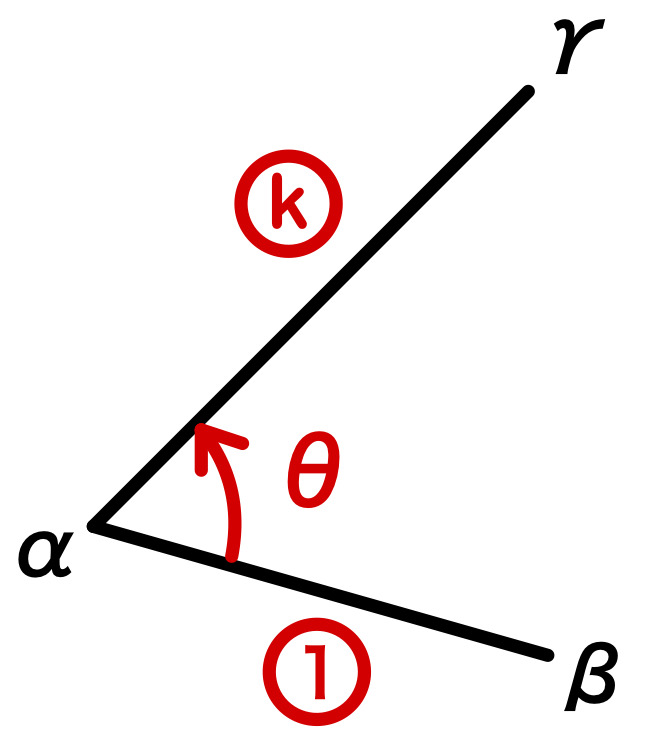
または
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)
\(z\) を点 \(1\) を中心に反時計回りに \(\displaystyle\frac{2\pi}{3}\) 回転した点が \(z_{1}\) より
\(z_{1}-1=\left(\cos\displaystyle\frac{2\pi}{3}+i\sin\displaystyle\frac{2\pi}{3}\right)(z-1)\)
よって \(z_{1}=\left(-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\right)z+\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
また,\(z_{1}\) を原点を中心に反時計回りに \(\displaystyle\frac{2\pi}{3}\) 回転した点が \(z_{2}\) より
\(z_{2}=\left(\cos\displaystyle\frac{2\pi}{3}+i\sin\displaystyle\frac{2\pi}{3}\right)z_{1}\)
\(z_{2}=\left(\cos\displaystyle\frac{2\pi}{3}+i\sin\displaystyle\frac{2\pi}{3}\right)\left\{\left(-\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\right)z+\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right\}\)
\(=\left(-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)z+\sqrt{3}i\)
さらに問2より
\(f(z)=\left(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{z_{2}}\)
\(=\left(\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{\left\{\left(-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)z+\sqrt{3}i\right\}}\)
したがって,
\(f(z)=\left(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{z}-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
問4
\(f(z)=-z-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\) のとき
問3より \(f(z)=\left(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{z}-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
\(-z-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i=\left(\displaystyle\frac{1}{2}+\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{z}-\displaystyle\frac{3}{2}-\displaystyle\frac{\sqrt{3}}{2}i\)
\(z=\left(-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)\overline{z}\)
ここで,\(x\),\(y\) を実数として \(z=x+yi\) とおくと
\(\overline{z}=x-yi\) より
\(x+yi=\left(-\displaystyle\frac{1}{2}-\displaystyle\frac{\sqrt{3}}{2}i\right)(x-yi)\)
\(\iff\) \(x+yi=\left(-\displaystyle\frac{1}{2}x-\displaystyle\frac{\sqrt{3}}{2}y\right)+\left(-\displaystyle\frac{\sqrt{3}}{2}x+\displaystyle\frac{1}{2}y\right)i\)
 よって
よって
\(\begin{cases}x=-\displaystyle\frac{1}{2}x-\displaystyle\frac{\sqrt{3}}{2}y\\y=-\displaystyle\frac{\sqrt{3}}{2}x+\displaystyle\frac{1}{2}y\end{cases}\)
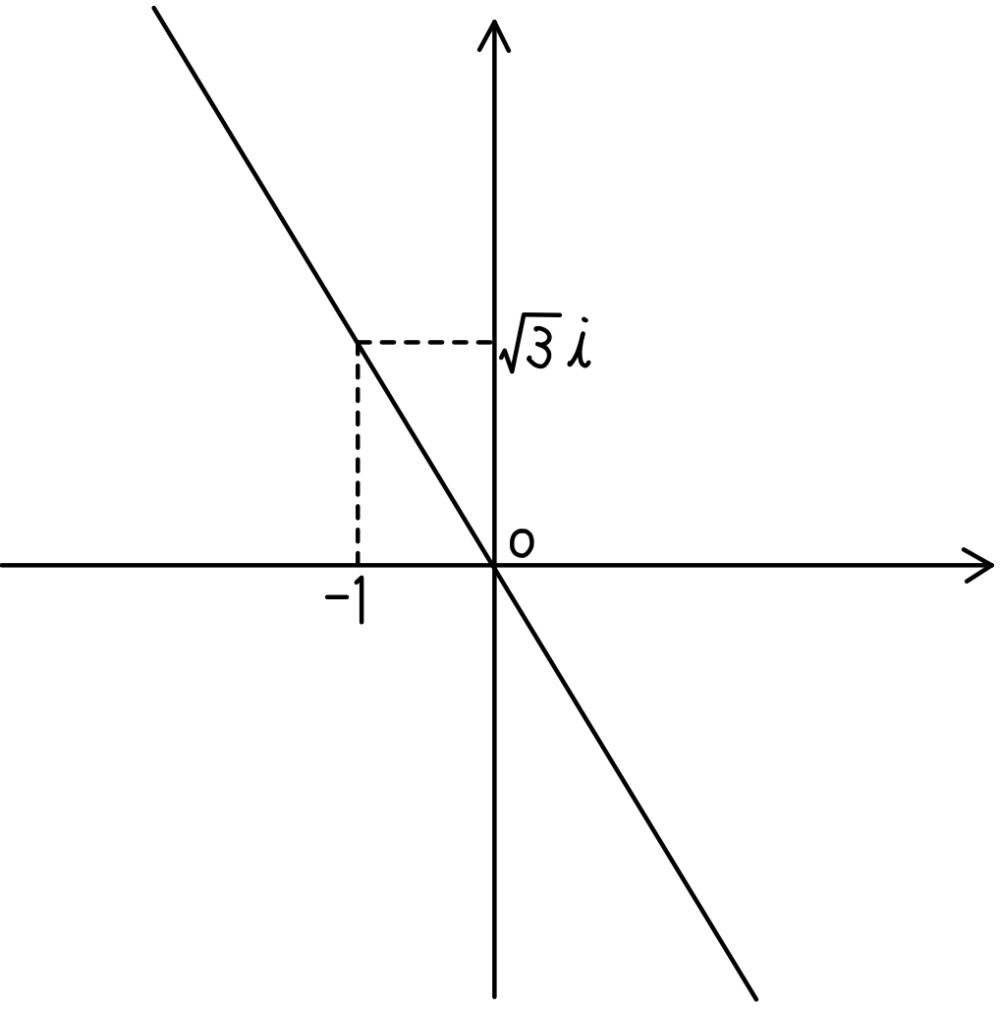
\(\iff\) \(y=-\sqrt{3}x\)
よって与式を表す複素数平面上の図形は右図の直線







コメント