 2024年入試問題
2024年入試問題 【2024京都大学・文系・第1問】対称性のある四面体の体積
空間図形。対称性のある四面体の立体の体積。合同、相似、外心、正弦定理など、1つ1つは基礎。問題・解答・解説速報。京大過去問演習。2024京都大学・文系・第1問(数学ⅠA)。
 2024年入試問題
2024年入試問題  2024年入試問題
2024年入試問題  共通テスト(センター試験)
共通テスト(センター試験)  東京大学
東京大学  図形の性質
図形の性質  分野まとめ
分野まとめ  図形の性質
図形の性質  図形の性質
図形の性質  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  図形の性質
図形の性質 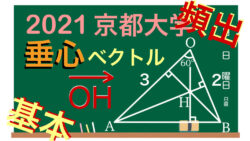 ベクトル
ベクトル 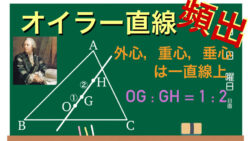 ベクトル
ベクトル