【2023東京大学・理科・第６問】
\(O\) を原点とする座標空間において，不等式 \(|x|≦1\)，\(|y|≦1\)，\(|z|≦1\) の表す立方体を考える．その立方体の表面のうち，\(z<1\) を満たす部分を \(S\) とする．
以下，座標空間内の \(2\) 点 \(A\) , \(B\) が一致するとき，線分 \(AB\) は点 \(A\) を表すものとし，その長さを \(0\) と定める．
(１) 座標空間内の点 \(P\) が次の条件( ⅰ )，( ⅱ )をともに満たすとき，点 \(P\) が動きうる範囲 \(V\) の体積を求めよ．
( ⅰ ) \(OP≦\sqrt{3}\)
( ⅱ ) 線分 \(OP\) と \(S\) は，共有点を持たないか，点 \(P\) のみを共有点に持つ．
(２) 座標空間内の点 \(N\) と点 \(P\) が次の条件 ( ⅲ )，( ⅳ )，( ⅴ ) をすべて満たすとき，点 \(P\) が動きうる範囲 \(W\) の体積を求めよ．必要ならば，\(\sin\alpha=\displaystyle\frac{1}{\sqrt{3}}\) を満たす実数 \(\alpha\) \(\left(0<\alpha<\displaystyle\frac{\pi}{2}\right)\) を用いてよい．
( ⅲ ) \(ON+NP≦\sqrt{3}\)
( ⅳ ) 線分 \(ON\) と \(S\) は共有点を持たない．
( ⅴ ) 線分 \(NP\) と \(S\) は，共有点を持たないか，点 \(P\) のみを共有点に持つ．
解答・解説
(１) 点 \(P\) が動きうる範囲 \(V\) の体積
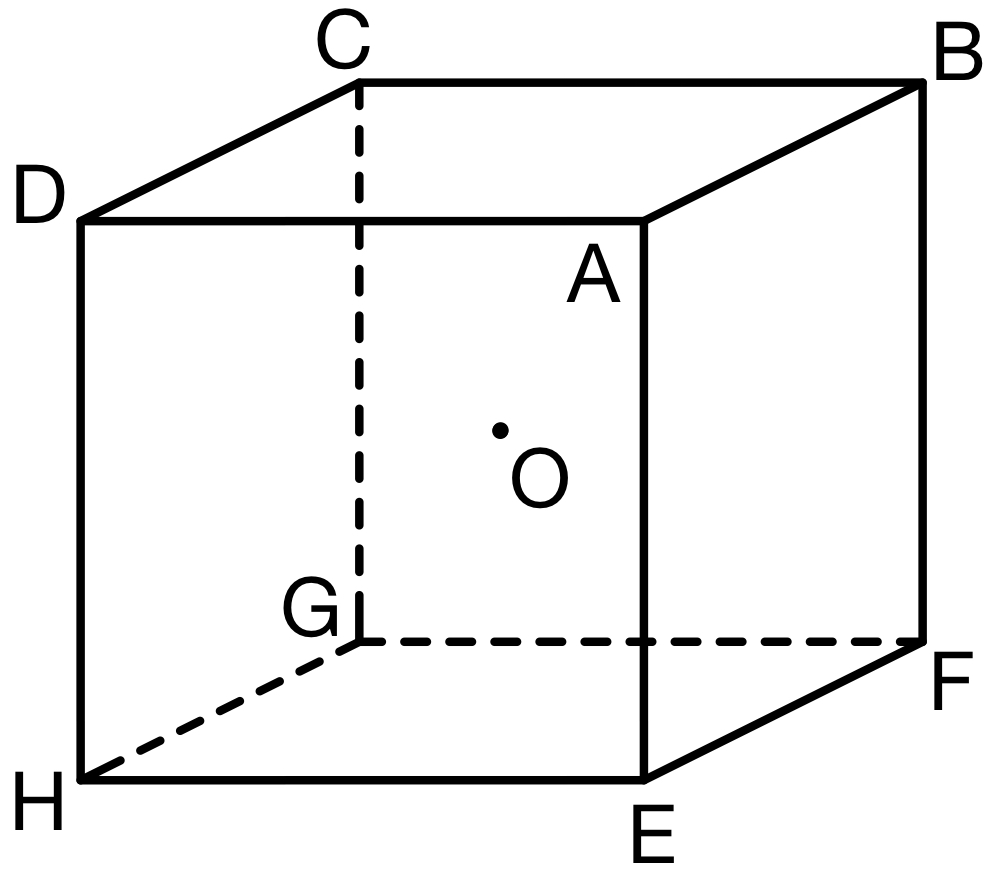
右図のように各点をとる．
立方体 \(ABCD-EFGH\) を，\(O-ABCD\)，\(O-ABFE\)，\(O-BCGF\)，\(O-CDHG\)，\(O-DAEH\)，\(O-EFGH\) の \(6\) つの四角錐に分ける．
求める体積 \(V\) は，\(O-ABCD\) 以外の \(5\) つの四角錐と，
中心 \(O\)，半径 \(\sqrt{3}\) の球を三角形 \(OAB\)，\(OBC\)，\(OCD\)，\(ODA\) で切断してできる小さい方の体積を合わせたもの．
したがって，
\(2^3\times\displaystyle\frac{5}{6}+\displaystyle\frac{4}{3}\pi\cdot\left(\sqrt{3}\right)^3\times \displaystyle\frac{1}{6}=\displaystyle\frac{20+2\sqrt{3}}{3}\)
(２) 点 \(P\) が動きうる範囲 \(W\) の体積
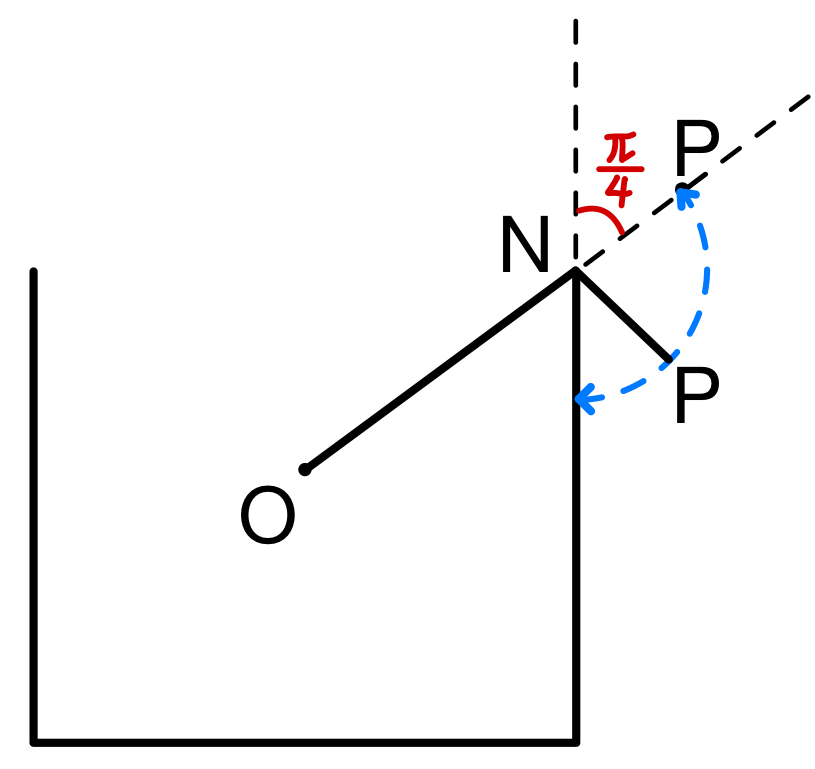点 \(N\) が線分 \(OP\) 上のとき，\(W\) は(１)の \(V\) と一致する．
\(W\) のうち，\(V\) に含まれない部分の体積を \(X\) とすると，
\(X\) は点 \(N\) が線分 \(AB\)，\(BC\)，\(CD\)，\(DA\) 上に存在し，点 \(P\) が \(V\) の外側に存在するときである．
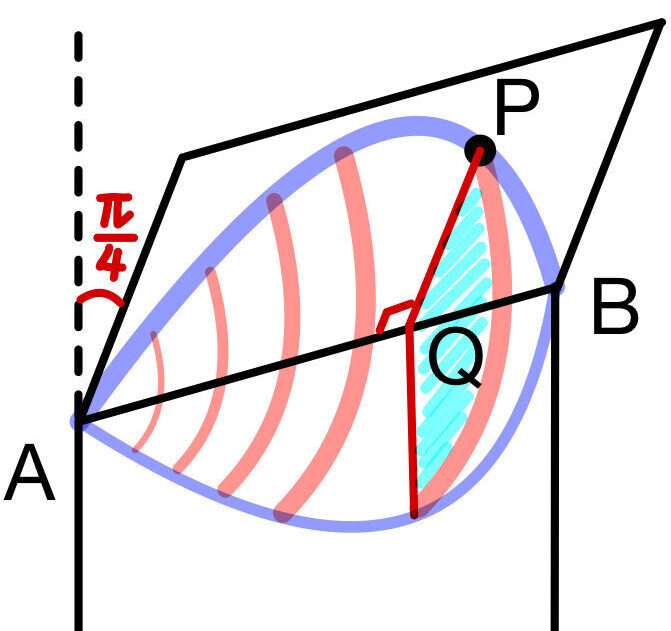図形の対称性から，点 \(N\) が線分 \(AB\)，\(BC\)，\(CD\)，\(DA\) 上にそれぞれあるときにできる体積はいずれも等しいので，
\(X\) のうち，点 \(N\) が線分 \(AB\) 上にあるときについて考える．
ここで，線分 \(AB\) に垂直となる平面 \(y=t\) ( \(-1≦t≦1\) ) における断面は
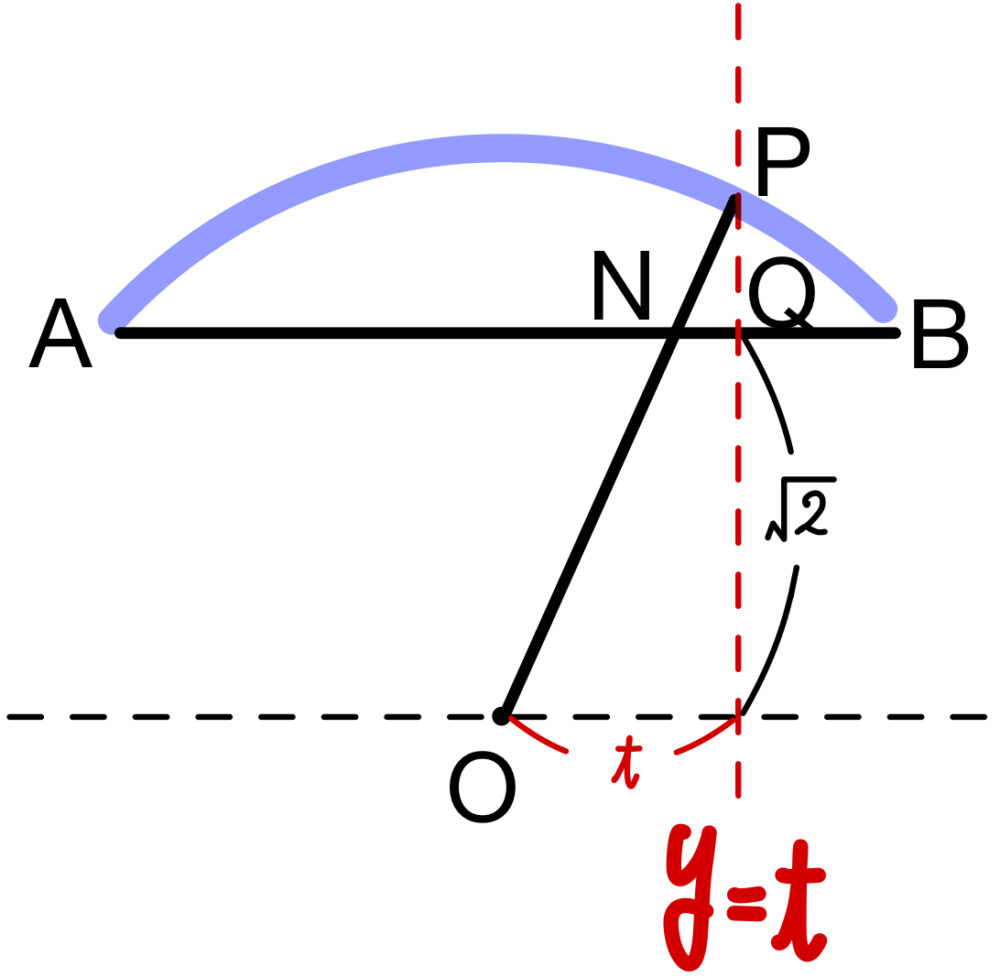右図の関係から
半径が \(\sqrt{3-t^2}-\sqrt{2}\) ，中心角 \(\displaystyle\frac{3\pi}{4}\) の扇形となるので
\(\displaystyle\frac{X}{4}=\displaystyle\int^{1}_{-1}\displaystyle\frac{1}{2}\left(\sqrt{3-t^2}-\sqrt{2}\right)^2\cdot\displaystyle\frac{3\pi}{4} dt\)
\(=\displaystyle\frac{3\pi}{4}\displaystyle\int^{1}_{0} \left(\sqrt{3-t^2}-\sqrt{2}\right)^2dt\)
\(=\displaystyle\frac{3\pi}{4}\displaystyle\int^{1}_{0} \left(5-t^2-2\sqrt{2}\cdot\sqrt{3-t^2}\right)dt\)
よって
\(X=3\pi\displaystyle\int^{1}_{0}(5-t^2) dt-6\sqrt{2}\pi \displaystyle\int^{1}_{0}\sqrt{3-t^2} dt\)
ここで
\(\displaystyle\int^{1}_{0}(5-t^2) dt=\Bigl[5t-\displaystyle\frac{1}{3}t^3\Bigr]^{1}_{0}=\displaystyle\frac{14}{3}\)
\(\displaystyle\int^{1}_{0}\sqrt{3-t^2} dt\) について
\(t=\sqrt{3}\sin \theta\) とおくと
\(\displaystyle\frac{dt}{d \theta}=\sqrt{3}\cos \theta\)，
\(t\)：\(0\) \(\rightarrow\) \(1\) のとき
\(\theta\)：\(0\) \(\rightarrow\) \(\alpha\) より
\(\displaystyle\int^{1}_{0}\sqrt{3-t^2} dt=\displaystyle\int^{\alpha}_{0}\sqrt{3}\cos\theta\cdot\sqrt{3}\cos\theta d \theta\)
\(=3\displaystyle\int^{\alpha}_{0}\cos^2 \theta d\theta\)
\(=\displaystyle\frac{3}{2}\displaystyle\int^{\alpha}_{0}(\cos 2\theta+1) d\theta\)
\(=\displaystyle\frac{3}{2}\Bigl[\displaystyle\frac{1}{2}\sin 2\theta+\theta\Bigr]^{\alpha}_{0}\)
\(=\displaystyle\frac{3}{2}\left(\displaystyle\frac{1}{2}\sin 2\alpha+\alpha\right)\)
\(\sin\alpha=\displaystyle\frac{1}{\sqrt{3}}\) より \(\cos\alpha=\displaystyle\frac{\sqrt{2}}{\sqrt{3}}\)
よって \(\sin 2\theta=2\sin\theta\cos\theta=\displaystyle\frac{2\sqrt{2}}{3}\) なので
\(\displaystyle\int^{1}_{0}\sqrt{3-t^2} dt=\displaystyle\frac{3}{2}\left(\displaystyle\frac{\sqrt{2}}{3}+\alpha\right)\)
ゆえに，
\(X=3\pi\times \displaystyle\frac{14}{3}-6\sqrt{2}\pi\times\displaystyle\frac{3}{2}\left(\displaystyle\frac{\sqrt{2}}{3}+\alpha\right)\)
\(=8\pi-9\sqrt{2}\pi\alpha\)
したがって求める体積は
\(W=V+X=\displaystyle\frac{20+2\sqrt{3}}{3}+8\pi-9\sqrt{2}\pi\alpha\)
\(W=\displaystyle\frac{20}{3}+\left(\displaystyle\frac{2\sqrt{3}}{3}+8-9\sqrt{2}\alpha\right)\pi\)
コメント