【問題1】
複素数平面 \(\alpha\)、\(\beta\) が \(| \alpha | = | \beta | = | \alpha – \beta | = 2\) を満たしているとき、次の値を求めよ.
(1) \(| \alpha+\beta |\)
(2) \(\displaystyle\frac{\alpha^{3}}{\beta^{3}}\)
(3) \(| \alpha^2+\beta^2 |\)
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
![]()
複素数平面の基本的な解法
複素数平面の問題は、基本的に次の3つのどれかで考えていきます.
① \(z\) のまま扱う
・\(|z|^2=z\cdot \overline{z}\)、\(z+\overline{z}\) は実数・・・などの性質を利用
② \(z=x+yi\) ( \(x , y\) は実数 ) とおいて計算
③ 極形式の利用
・\(z=r(\cos \theta+i\sin \theta)\) とおいて
ド・モアブルの定理などを利用
ド・モアブルの定理
\(n\) が整数のとき
\((\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta\)
複素数の絶対値についての性質
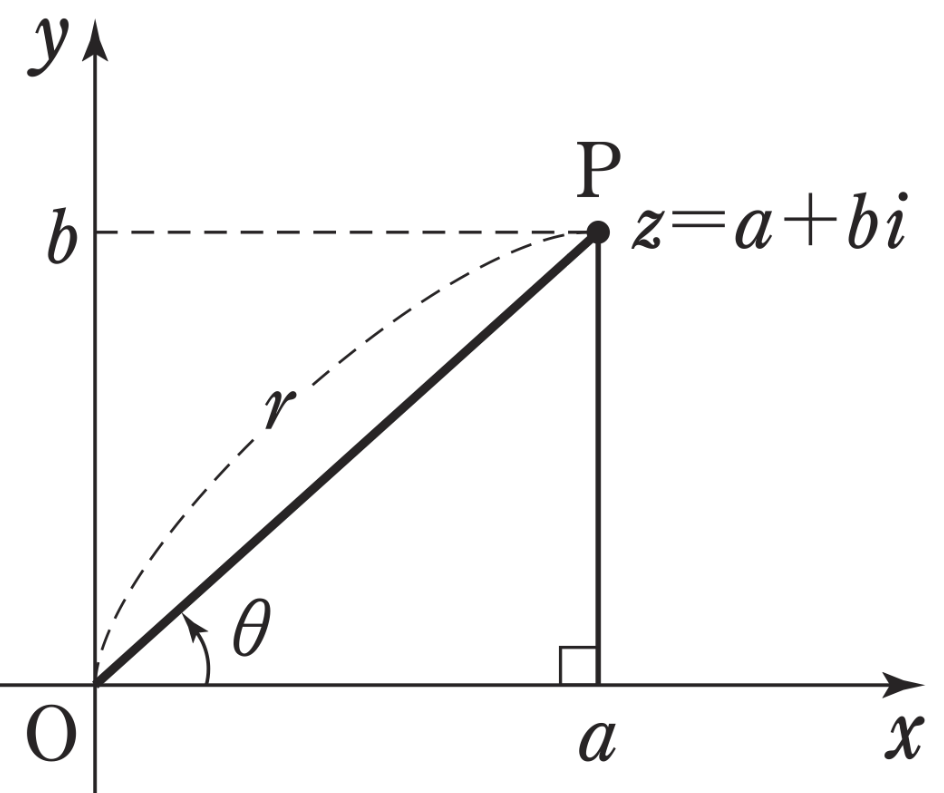
・\(| \alpha |\) とは、原点 \(O\) と点 \(\alpha\) の距離
※\(\alpha = a+bi\) ( \(a , b\) は実数 ) のとき、\(| \alpha |=\sqrt{a^2+b^2}\)
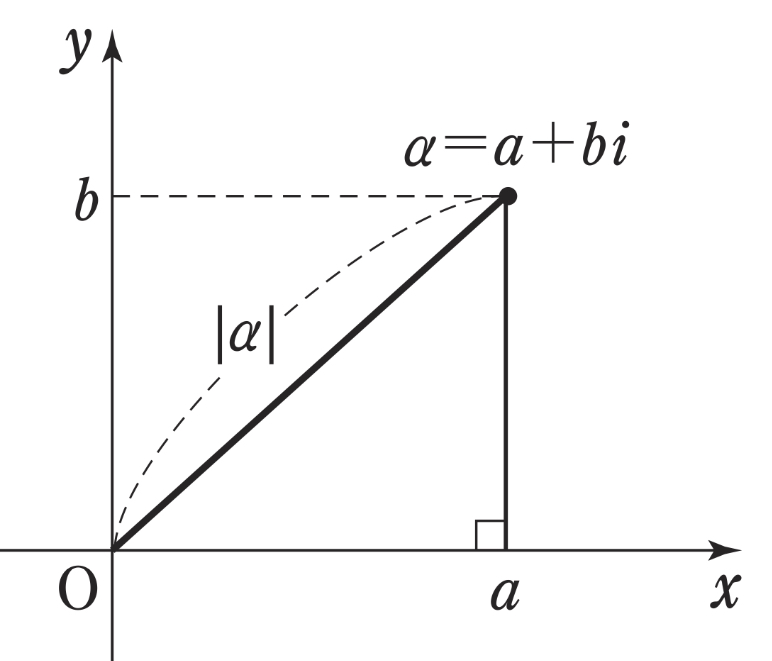
☆\(| \beta – \alpha|\) は \(2\) 点 \(\alpha\)、\(\beta\) の距離 ←重要
・\(| \alpha |≧0\) 特に、\(| \alpha | = 0 \iff \alpha = 0\)
・\(| \alpha | = | -\alpha | = | \overline{\alpha} |\)
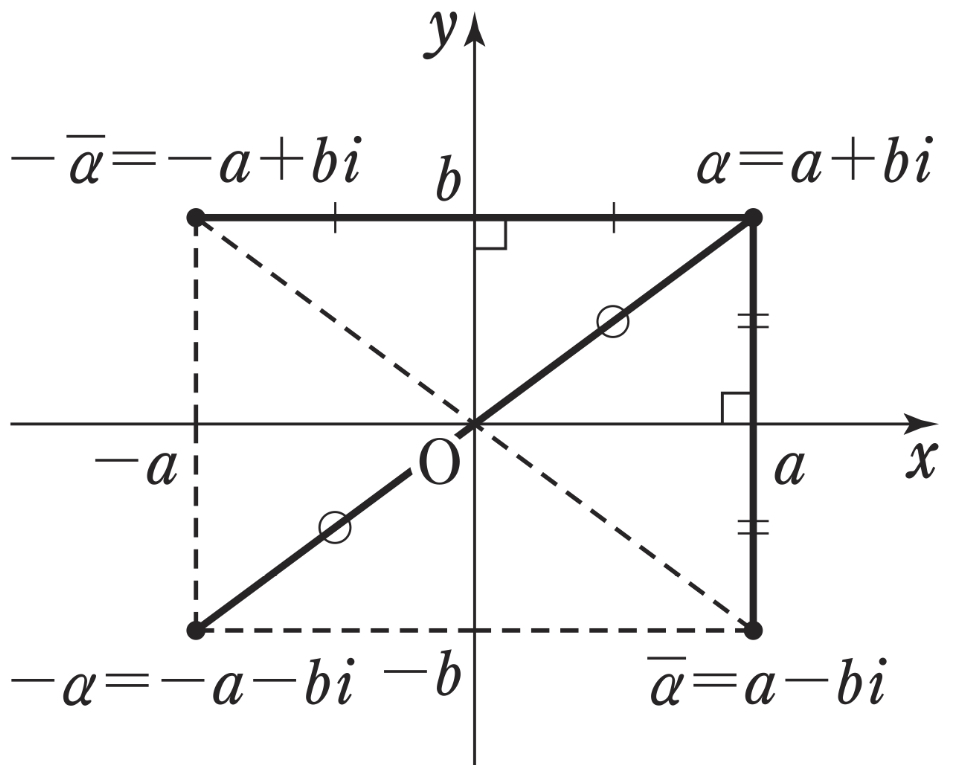
☆\(| \alpha |^2 = \alpha \cdot \bar{\alpha}\) ←超重要!
・\(| \alpha\beta | = | \alpha |\cdot| \beta |\)
・\(\left|\displaystyle\frac{\alpha}{\beta}\right| = \displaystyle\frac{| \alpha |}{| \beta |}\)
解答
(1) 条件 \(| \alpha-\beta | = 2\) より各辺を \(2\) 乗して
\(| \alpha-\beta |^2 = 4\)
\(( \alpha – \beta )(\overline{\alpha} – \overline{\beta}) = 4\)
\(( \alpha – \beta )(\overline{\alpha} – \overline{\beta}) = 4\)
\(\alpha \cdot \overline{\alpha} – \alpha \cdot \overline{\beta} – \overline{\alpha} \cdot \beta + \beta \overline{\beta} = 4\)
\(\alpha \cdot \overline{\alpha} = | \alpha |^2 = 2^2 = 4\)、\(\beta \cdot \overline{\beta} = | \beta |^2 = 2^2 = 4\) より
\(4-\alpha \cdot \overline{\beta} – \overline{\alpha} \cdot \beta +4=4\)
\(\alpha \cdot \overline{\beta} + \overline{\alpha} \cdot \beta =4\) ・・・①
このとき、
\(| \alpha+\beta |^2 \\= ( \alpha+\beta )(\overline{\alpha}+\overline{\beta })\\=\alpha \cdot \overline{\alpha}+\alpha \cdot \overline{\beta} + \overline{\alpha} \cdot \beta+\beta\cdot \overline{\beta}\)
\(| \alpha |^2=| \beta |^2=4\) と①より
\(| \alpha+\beta |^2=12\)
よって、\(| \alpha+\beta |>0\) なので、\(| \alpha+\beta |=2\sqrt{3}\)
(2) \(| \alpha | = 2\) より
\(\alpha \cdot \overline{\alpha}=| \alpha |^2=2^2=4\)
\(\alpha\not=0\) より \(\bar{\alpha}=\displaystyle\frac{4}{\alpha}\)
同様に考え、\(\overline{\beta}=\displaystyle\frac{4}{\beta}\) を ① に代入すると
\(\alpha \cdot \displaystyle\frac{4}{\beta} + \displaystyle\frac{4}{\alpha} \cdot \beta =4\)
\(\displaystyle\frac{\alpha}{\beta}+\displaystyle\frac{\beta}{\alpha}=1\) ・・・②
辺々に \(\displaystyle\frac{\alpha}{\beta}\) をかけて
\(\left(\displaystyle\frac{\alpha}{\beta}\right)^2-\displaystyle\frac{\alpha}{\beta}+1=0\)
解の公式より( \(x^2-x+1=0\ )のように考えて )
\(\displaystyle\frac{\alpha}{\beta}=\displaystyle\frac{1\pm\sqrt{3}i}{2}=\cos \left(\pm \displaystyle\frac{\pi}{3}\right)+i\sin \left(\pm \displaystyle\frac{\pi}{3}\right)\)
ド・モアブルの定理より、
\(\displaystyle\frac{\alpha^{3}}{\beta^{3}}=\left(\displaystyle\frac{\alpha}{\beta}\right)^3=\cos (\pm\pi)+i\sin (\pm\pi)=-1\)
(3) ②の両辺を \(\alpha\beta\) 倍して
\(\alpha^2+\beta^2=\alpha\beta\)
\(| \alpha^2+\beta^2 | = | \alpha\beta | = | \alpha |\cdot| \beta | = 4\)
![]()
別解:図形的なアプローチ
条件 \(| \alpha | = | \beta | = | \alpha-\beta | = 2\) において、
\(| \alpha |\) とは、原点 \(O\) と点 \(\alpha\) の距離、
\(| \beta |\) とは、原点 \(O\) と点 \(\beta\) の距離、
\(| \alpha – \beta|\) は \(2\) 点 \(\alpha\)、\(\beta\) の距離 であるから、
\(3\) 点、\(O\)、\(\alpha\)、\(\beta\) でできる図形は、正三角形となる.
また、\(\alpha+\beta\) は、下図の点\(C\) ( 四角形OACB は平行四辺形 ) を満たす点を表す.
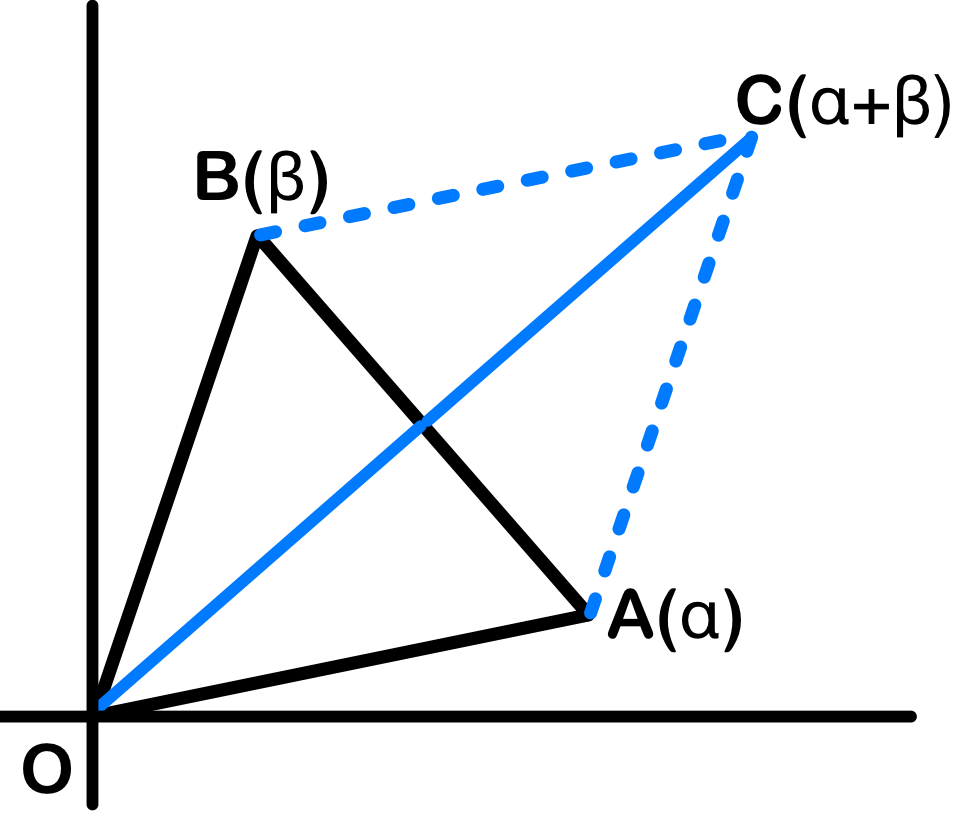
したがって、
(1)の \(| \alpha+\beta |\) は上図の線分 \(OC\) の長さを意味する
よって、\(OC=| \alpha+\beta |=2\sqrt{3}\)
(2) (1)より、△OABは正三角形なので
\(arg\alpha=\theta\) とおくと、\(arg\beta=\theta\pm\displaystyle\frac{\pi}{3}\) となる
\(| \alpha | = | \beta |\) より \(| \alpha |^3 = | \beta |^3\)
つまり、\(| \alpha^3 | = | \beta^3 |\) となる.
また、\(arg\alpha^3=3\theta\)、\(arg\beta^3=3\theta\pm\pi\) であるから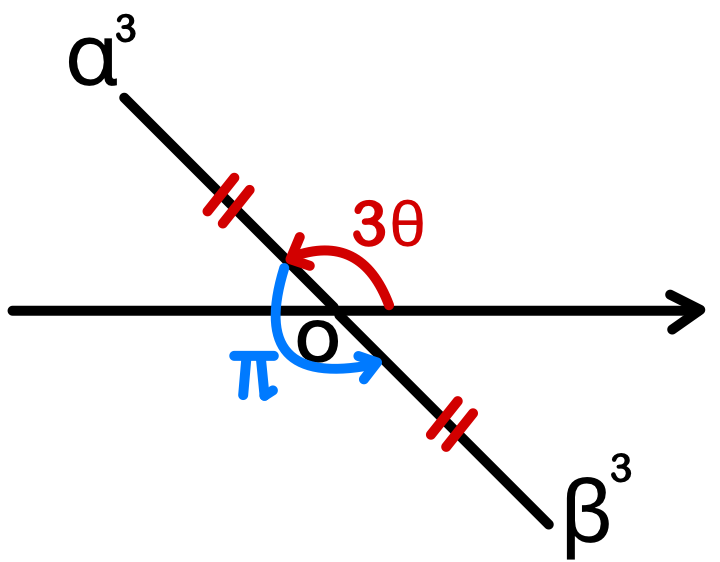
\(\alpha^3=-\beta^3 \)
\(\beta\not=0\) より \(\displaystyle\frac{\alpha^{3}}{\beta^{3}}=-1\)
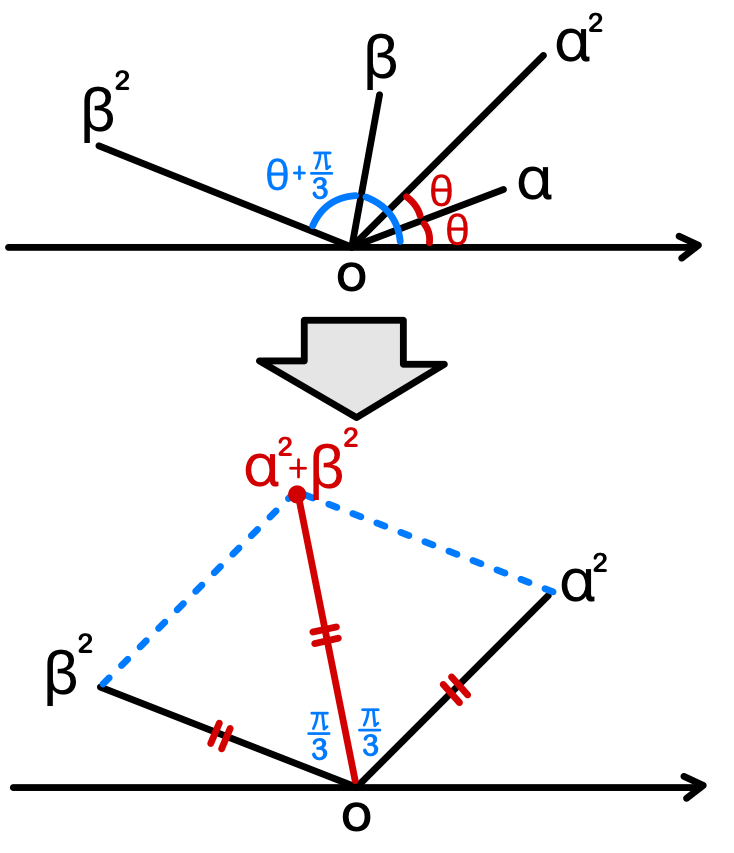
(3) \(arg\alpha=\theta\) とおくと、\(arg\beta=\theta\pm\displaystyle\frac{\pi}{3}\)
\(arg\alpha^2=2\theta\)、\(arg\beta^2=2\theta\pm\displaystyle\frac{2\pi}{3}\) となる
よって、\(\arg\beta^2-\alpha^2=\pm\displaystyle\frac{2\pi}{3}\)
また、\(| \alpha^2 | = | \beta^2 |\)
したがって、各点は下図のようになり、\(| \alpha^2+\beta^2 |=| \alpha^2 |=4\)








コメント