【問題2】
【1】 次の問に答えよ.
(1) 複素数 \(z\) が、\(z^3=1\)、\(z\not=1\) を満たすとき
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}\) の値を求めよ.
(2) 複素数 \(z\) が、\(z^5=1\)、\(z\not=1\) のとき、
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}+\displaystyle\frac{1}{1-z^3}+\displaystyle\frac{1}{1-z^4}\) の値を求めよ.
【2】 次の問に答えよ.
(1) 複素数 \(z\) が、\(z^3=1\)、\(z\not=1\) を満たすとき、\((1-z)(1-z^2)\) の値を求めよ.
(2) \(\alpha=\cos \displaystyle\frac{2\pi}{5}+i\sin \displaystyle\frac{2\pi}{5}\) として、\(x\) についての恒等式 \((x-\alpha)(x-\alpha^2)(x-\alpha^3)(x-\alpha^4)=x^4+x^3+x^2+x+1\) を示せ.
(3) \(n\) は \(3\) 以上の自然数とする.
\(\beta=\cos \displaystyle\frac{2\pi}{n}+i\sin \displaystyle\frac{2\pi}{n}\) として、
等式 \((1-\beta)(1-\beta^2)(1-\beta^3)\cdots(1-\beta^{n-1})=n\) を示せ.
(4) \(\displaystyle\frac{n}{2^{n-1}}=\sin \displaystyle\frac{\pi}{n}\sin \displaystyle\frac{2\pi}{n}\cdots\sin \displaystyle\frac{(n-1)\pi}{n}\) を示せ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
1の n 乗根について
【\(1\) の \(n\) 乗根について】
① \(z^n=1\) の解について
・解は、\(z_{k}=\cos \displaystyle\frac{2k}{n} \pi+i\sin \displaystyle\frac{2k}{n} \pi \)
(\(k = 0 , 1 , 2 , \cdots , n-1\))
・\(1 , z , z^2 , z^3 , \cdots , z^{n-1}\) は異なる \(n\) 個の解
・正 \(n\) 角形の頂点となる
② \(z+\overline{z}=2\cos \displaystyle\frac{2k}{n} \pi \) (実数)
③ \(| z | = 1 \iff z\cdot \overline{z}=1 \iff \overline{z}=\displaystyle\frac{1}{z}\)
④ \(z^n=1 \iff (z-1)(z^{n-1}+z^{n-2}+\cdots+z+1)=0\)
考え方・解答
【1】 次の問に答えよ.
(1) 複素数 \(z\) が、\(z^3=1\)、\(z\not=1\) を満たすとき
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}\) の値を求めよ.
(2) 複素数 \(z\) が、\(z^5=1\)、\(z\not=1\) のとき、
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}+\displaystyle\frac{1}{1-z^3}+\displaystyle\frac{1}{1-z^4}\) の値を求めよ.
【1】について
(1)に関しては、素直に通分し、計算していく方法でももちろん答えにたどりつく.
しかしその方法では、(2)の問題はなかなか大変である.(さらに言うと、もう少し値が大きくなったときに、非常に大変な計算になる.)
そこで、\(z^n=1\) であることを上手に利用した解法を考える.
【1】 解答
(1) \(\displaystyle\frac{1}{1-z^2}\) の分母分子に、\(z\) をかけると、\(z^3=1\) より
\(\displaystyle\frac{1}{1-z^2}=\displaystyle\frac{z}{z-z^3}=\displaystyle\frac{z}{z-1}\)
よって、
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}\\=\displaystyle\frac{1}{1-z}+\displaystyle\frac{z}{z-1}\\=\displaystyle\frac{-1}{z-1}+\displaystyle\frac{z}{z-1}=1\)
(2)に関しても、(1)と同様に考えていく.
\(\displaystyle\frac{1}{1-z^3}\) の分母分子に、\(z^2\) をかけ、
\(\displaystyle\frac{1}{1-z^4}\) の分母分子に、\(z\) をかけると
\(\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}+\displaystyle\frac{1}{1-z^3}+\displaystyle\frac{1}{1-z^4}\\=\displaystyle\frac{1}{1-z}+\displaystyle\frac{1}{1-z^2}+\displaystyle\frac{z^2}{z^2-1}+\displaystyle\frac{z}{z-1}\\=2\)
![]()
【2】 (1)~(3)について
【2】 次の問に答えよ.
(1) 複素数 \(z\) が、\(z^3=1\)、\(z\not=1\) を満たすとき、\((1-z)(1-z^2)\) の値を求めよ.
(2) \(\alpha=\cos \displaystyle\frac{2\pi}{5}+i\sin \displaystyle\frac{2\pi}{5}\) として、\(x\) についての恒等式 \((x-\alpha)(x-\alpha^2)(x-\alpha^3)(x-\alpha^4)=x^4+x^3+x^2+x+1\) を示せ.
(3) \(n\) は \(3\) 以上の自然数とする.
\(\beta=\cos \displaystyle\frac{2\pi}{n}+i\sin \displaystyle\frac{2\pi}{n}\) として、
等式 \((1-\beta)(1-\beta^2)(1-\beta^3)\cdots(1-\beta^{n-1})=n\) を示せ.
(4) \(\displaystyle\frac{n}{2^{n-1}}=\sin \displaystyle\frac{\pi}{n}\sin \displaystyle\frac{2\pi}{n}\cdots\sin \displaystyle\frac{(n-1)\pi}{n}\) を示せ.
(1)であれば、単純に計算すれば求めることはそこまで難しくはない。
しかし、単純な計算だけで求めていると、(2)、(3)のような問題で太刀打ちできなくなります。
このタイプの問題は頻出ですから、一般的な求め方をしっかりとマスターしておきましょう!
上のPointの
① \(z^n=1\) の解について
・\(1 , z , z^2 , z^3 , \cdots , z^{n-1}\) は異なる \(n\) 個の解
④ \(z^n=1 \iff (z-1)(z^{n-1}+z^{n-2}+\cdots+z+1)=0\) を利用する。
\(z^n=1\) のとき
\(1 , z , z^2 , z^3 , \cdots , z^{n-1}\) は \(x^n=1\) の解となる.
この \(n\) この解はそれぞれ偏角が互いに異なるので、異なる \(n\) 個の解でるから、
\(x^n-1=(x-1)(x-z)(x-z^2)(x-z^3)\cdots(x-z^{n-1})\) ・・・(ア)
また、\(x^n-1=0=(x-1)(x^{n-1}+x^{n-2}+ \cdots +x+1)\) ・・・(イ) より
(ア)、(イ)から
\((x-1)(x-z)(x-z^2)(x-z^3)\cdots(x-z^{n-1})=(x-1)(x^{n-1}+x^{n-2}+ \cdots +x+1)\)
\(z\not=1\) のとき、
\((x-z)(x-z^2)(x-z^3)\cdots(x-z^{n-1})=x^{n-1}+x^{n-2}+ \cdots +x+1\) ・・・(ウ)
(1)については、(ウ)において、\(n=3\) のときであるから、
\((x-z)(x-z^2)=x^2+x+1\)
これに \(x=1\) を代入して
\((1-z)(1-z^2)=1^2+1+1=3\)
(2)については、
ド・モアブルの定理
\(n\) が整数のとき
\((\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta\)
を利用すると、
\(\alpha^n=\left(\cos \displaystyle\frac{2\pi}{5}+i\sin \displaystyle\frac{2\pi}{5}\right)^n=\cos 2\pi+i\sin 2\pi=1\)
(ウ)において、\(n=5\) のときを考えると
\((x-\alpha)(x-\alpha^2)(x-\alpha^3)(x-\alpha^4)=x^4+x^3+x^2+x+1\) が成立する.
(3) (2)と同様、ド・モアブルの定理より
\(\beta^n=\left(\cos \displaystyle\frac{2\pi}{n}+i\sin \displaystyle\frac{2\pi}{n}\right)^n=\cos 2\pi+i\sin 2\pi=1\)
\((x-z)(x-z^2)(x-z^3)\cdots(x-z^{n-1})=x^{n-1}+x^{n-2}+ \cdots +x+1\) ・・・(ウ)
(ウ)の式において、\(x=1\) を代入すると
等式 \((1-\beta)(1-\beta^2)(1-\beta^3)\cdots(1-\beta^{n-1})=n\) が成立する.
【2】の(4)について
上で確認したPointの
① \(1\) の \(n\) 乗根について
・\(1 , z , z^2 , z^3 , \cdots , z^{n-1}\) は異なる \(n\) 個の解
・正 \(n\) 角形の頂点 を利用する
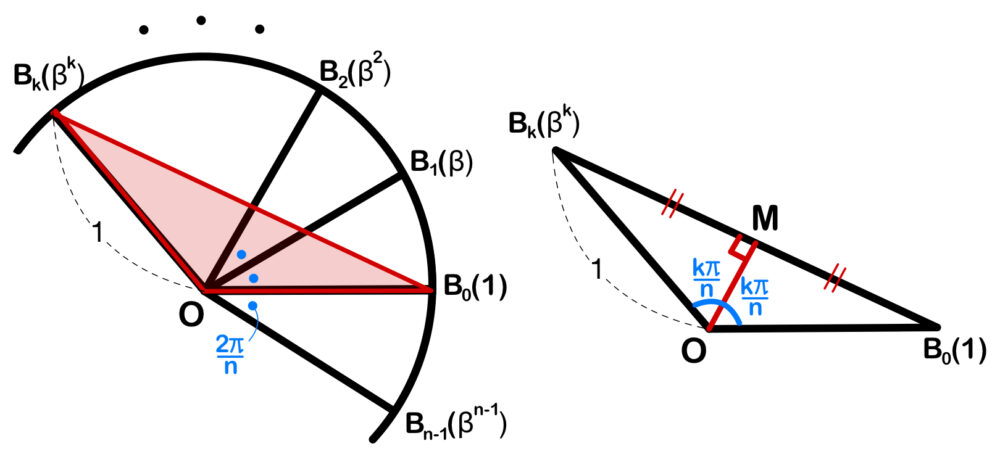
\(3\) 点 \(O(0)\)、\(B_{0}(1)\)、\(B_{k}(\beta^k)\) とおく.
このとき、\(OB_{0}=OB_{k}=1\)、\(B_{0}B_{k}=|1-\beta^k|\)、\(arg∠B_{0}O B_{k}=\displaystyle\frac{2k\pi}{n}\)
また、\(B_{0}\) と \(B_{k}\) の中点を \(M\) とすると、
\(arg∠B_{k}OM=\displaystyle\frac{k\pi}{n}\) より
\(\sin ∠B_{k}OM=\sin \displaystyle\frac{k\pi}{n}=\displaystyle\frac{B_{k}M}{OB_{k}}= B_{k}M \)
\( B_{0}B_{k} = 2B_{k}M \) より
\(\sin \displaystyle\frac{k\pi}{n}=\displaystyle\frac{|1-\beta^k|}{2}\) ・・・(エ)
(エ)に \(k = 1 , 2 , \cdots , n-1\) を代入し、それぞれをかけると
\(\sin \displaystyle\frac{\pi}{n}\times\sin \displaystyle\frac{2\pi}{n}\times \cdots \times \sin \displaystyle\frac{(n-1)\pi}{n}\\=\displaystyle\frac{|1-\beta|}{2}\times \displaystyle\frac{|1-\beta^2|}{2}\times \cdots \times\displaystyle\frac{|1-\beta|^{n-1}}{2}\\=\displaystyle\frac{|(1-\beta)(1-\beta^2)\cdots(1-\beta^{n-1})|}{2^{n-1}}\) となり、
(3)の結果から \((1-\beta)(1-\beta^2)(1-\beta^3)\cdots(1-\beta^{n-1})=n\) であるから、
\(\displaystyle\frac{n}{2^{n-1}}=\sin \displaystyle\frac{\pi}{n}\sin \displaystyle\frac{2\pi}{n}\cdots\sin \displaystyle\frac{(n-1)\pi}{n}\) が成立する.









コメント