【2021京都大学・理系】
\(a\) を \(1\) より大きい定数とする．微分可能な関数 \(f(x)\) が \(f(a)=af(1)\) を満たすとき，曲線 \(y=f(x)\) の接線で原点 \((0,0)\) を通るものが存在することを示せ．
平均値の定理
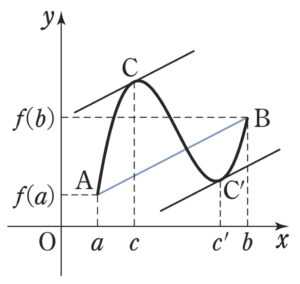関数 \(f(x)\) が閉区間 \([a,b]\) で連続で，
開区間 \((a,b)\) で微分可能ならば，
\(\displaystyle\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\) ， \(a<c<b\)
を満たす実数 \(c\) が存在する．
平均値の定理は，不等式の証明や極限を求めるとき，また本問のような〇〇が存在するといった存在証明の時にも利用されます！
解答・解説
\(f(a)=af(1)\) , \(a>1\) より
\(\displaystyle\frac{f(a)}{a}=\displaystyle\frac{f(1)}{1}\) ・・・①
\(x>0\) において \(g(x)=\displaystyle\frac{f(x)}{x}\) とおくと，
\(g^{\prime}(x)=\displaystyle\frac{xf^{\prime}(x)-f(x)}{x^2}\)
\(1≦x≦a\) において平均値の定理を用いると
\(\displaystyle\frac{g(a)-g(1)}{a-1}=g^{\prime}(c)\) , \(1<c<a\)
をみたす実数 \(c\) が存在する．
①より \(g(a)=g(1)\) であるから，\(g^{\prime}(c)=0\)
よって，\(\displaystyle\frac{cf^{\prime}(c)-f(c)}{c^2}=0\)
\(cf^{\prime}(c)-f(c)=0\) ・・・②
ここで，曲線 \(y=f(x)\) 上の点 \((c,f(c))\) における接線の方程式は
\(y-f(c)=f^{\prime}(c)(x-c)\)
\(y=f^{\prime}(c)x-\left\{cf^{\prime}(c)-f(c)\right\}\)
②より \(y=f^{\prime}(c)x\)
これは原点を通る直線である．
したがって，曲線 \(y=f(x)\) の接線で原点を通るものが存在する．
コメント