【問題5】
複素数 \(z_{1}\)、\(z_{2}\) があって、\(| z_{1} | = | z_{2} | = 1\)、\(arg z_{1}=\theta_{1}\)、\(arg z_{2}=\theta_{2}\) \(\left(0≦\theta_{1}<\theta_{2}≦\displaystyle\frac{\pi}{4}\right)\) とする.
\(w_{1}=z_{1}+z_{2}\)、\(w_{2}=z_{1}z_{2}\)、\(w_{3}=\displaystyle\frac{z_{2}}{z_{1}}\) とするとき、次の問に答えよ.
ただし、複素数平面の原点を \(O\) とする.
(1) \(w_{1}\)、\(w_{2}\)、\(w_{3}\) の偏角を求めよ.
(2) 線分 \(Ow_{3}\) が \(∠w_{1}Ow_{2}\) の二等分線となるとき、\(|w_{1}|\) を \(\theta_{1}\) で表せ.
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
複素数の積と絶対値、偏角
\(z_{1}=r_{1}(\cos \theta_{1}+i\sin \theta_{1})\)、\(z_{2}=r_{2}(\cos \theta_{2}+i\sin \theta_{2})\) のとき
- \(z_{1}z_{2} = r_{1}r_{2}\left\{\cos (\theta_{1}+\theta_{2})+i\sin (\theta_{1}+\theta_{2})\right\}\)
- \(| z_{1}z_{2} | = r_{1}r_{2}\)
- \(arg z_{1}z_{2} = arg z_{1}+arg z_{2}\)
複素数の商と絶対値、偏角
\(z_{1}=r_{1}(\cos \theta_{1}+i\sin \theta_{1})\)、\(z_{2}=r_{2}(\cos \theta_{2}+i\sin \theta_{2})\) のとき
- \(\displaystyle\frac{z_{1}}{z_{2}} = \displaystyle\frac{r_{1}}{r_{2}}\left\{\cos (\theta_{1}-\theta_{2})+i\sin (\theta_{1}-\theta_{2})\right\}\)
- \(\left| \displaystyle\frac{z_{1}}{z_{2}}\right| = \displaystyle\frac{r_{1}}{r_{2}}\)
- \(arg \displaystyle\frac{z_{1}}{z_{2}} = arg z_{1}-arg z_{2}\)
解答
(1) \(| z_{1} | = | z_{2} | = 1\)、\(w_{1}=z_{1}+z_{2}\) より、\(4\) 点 \(O\)、\(z_{1}\)、\(z_{2}\)、\(w_{1}\) は、下図のようなひし形の頂点となる.
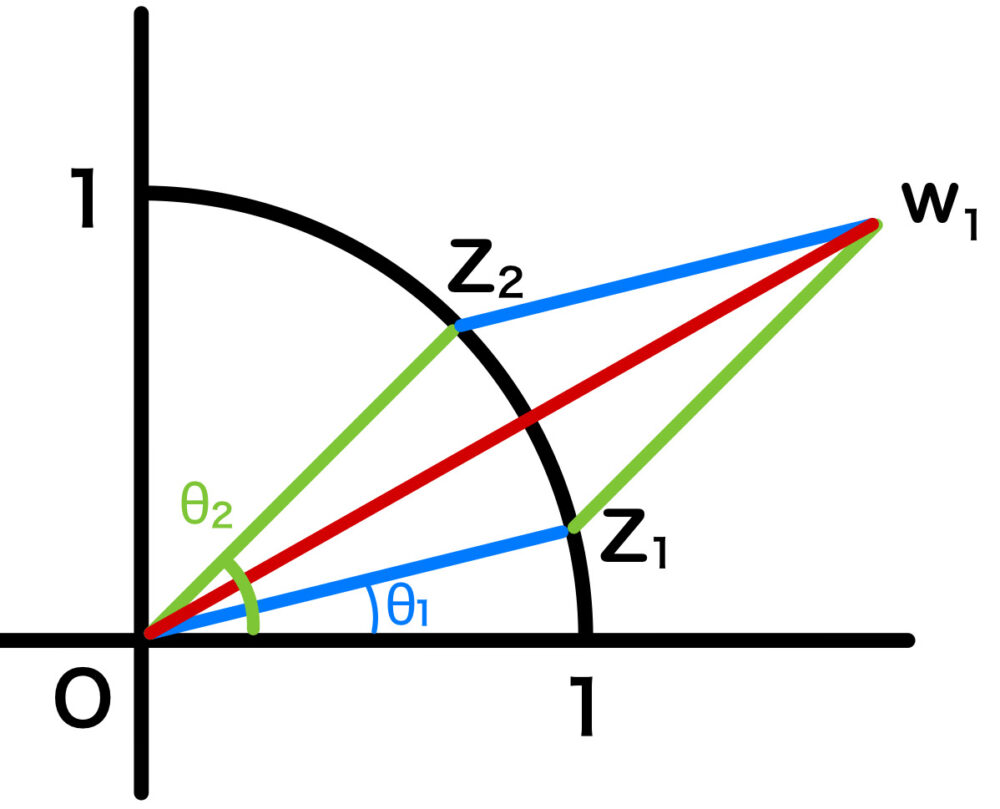
よって、\(arg w_{1}=\displaystyle\frac{\theta_{1}+\theta_{2}}{2}\)
また、\(w_{2}=z_{1}z_{2}=\cos (\theta_{1}+\theta_{2})+i\sin (\theta_{1}+\theta_{2})\) で、(1)の結果より
\(arg w_{2}=\theta_{1}+\theta_{2}\)
\(w_{3}=\displaystyle\frac{z_{2}}{z_{1}} = \cos (\theta_{2}-\theta_{1})+i\sin (\theta_{2}-\theta_{1})\) より
\(arg w_{3}=\theta_{2}-\theta_{1}\)
(2) \(arg w_{3}=\displaystyle\frac{arg w_{1}+arg w_{2}}{2}\) より
\(\theta_{2}-\theta_{1}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{\theta_{1}+\theta_{2}}{2}+\theta_{1}+\theta_{2}\right)\)
よって、\(\theta_{2}=7\theta_{1}\)
このとき、\(∠z_{1}Oz_{2}=\theta_{2}-\theta_{1}=6\theta_{1}\) なので、
\(∠z_{1}Ow_{1}=3\theta_{1}\)
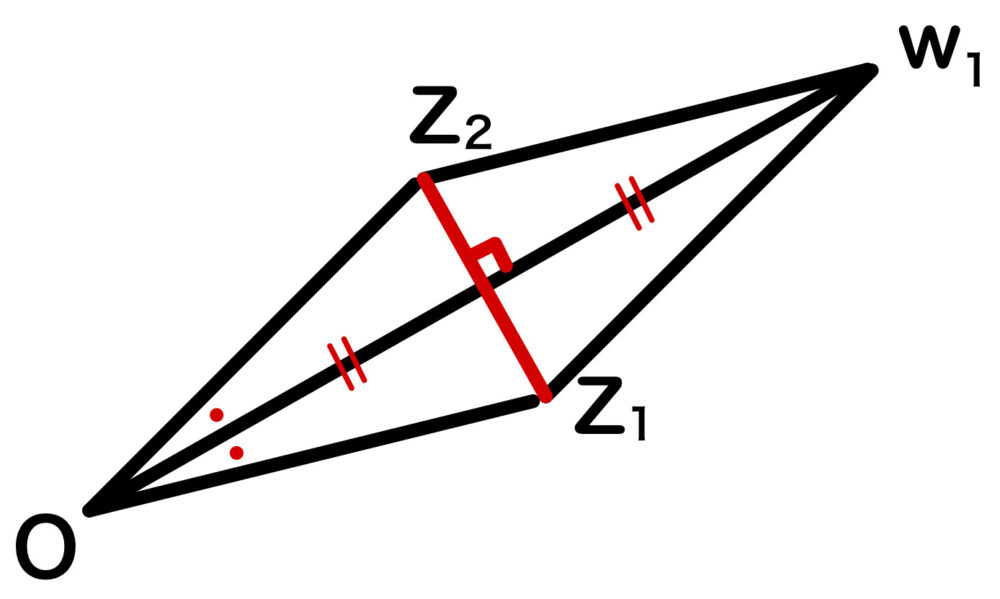
\(\cos 3\theta_{1}=\displaystyle\frac{\displaystyle\frac{1}{2}| w_{1} |}{| z_{1} |}=\displaystyle\frac{1}{2}| w_{1} |\)
したがって、\(| w_{1} |=2\cos 3\theta_{1}\)









コメント