三角関数のみの様々な積分について

※ 基本的公式レベルの問題を除き

$Q1$ ．三角・指数・対数関数があるか？　☞　YES！

$Q4$ ．三角関数が入っているか？　☞　YES！

$Q5$ ．三角関数のみか？　☞　YES！

のパターン(三角関数の積分)についての解法まとめのページになっています！

【このページで扱う例題】

①〜③の不定積分を求めよ．

①　 $\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx$

②　 $\displaystyle\int \displaystyle\sin^2 x\enspace dx$

③　 $\displaystyle\int \displaystyle\sin 3x\cos 2x\enspace dx$

④～⑥の定積分を計算せよ．

④　

$\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x \enspace dx$

⑤　

$\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^5x \enspace dx$

⑥　 $\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x\cos^2x \enspace dx$

《発展問題》

$\displaystyle\int\displaystyle\frac{5}{3\sin x+4\cos x}\enspace dx$

$(\sin x)^n\cos x$ , $(\cos x)^n\sin x$ の形
1. $t=\sin x$ , $\cos x$ と置換する
  1. 例題①
半角・積和の公式を利用して次数下げ
1. ２倍角の公式
  1. 例題②
2. 《積和の公式》
  1. 例題③
$\displaystyle\int^\frac{\pi}{2}_{0}\sin^nx\enspace dx$ について
発展問題： $t=\tan\displaystyle\frac{x}{2}$ と置換

$(\sin x)^n\cos x$ , $(\cos x)^n\sin x$ の形

$t=\sin x$ , $\cos x$ と置換する

例題①

不定積分

$\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx$ を求めよ．

$t=\sin x$ とおくと $dt=\cos x dx$ より

$\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx= \displaystyle\int \displaystyle t^3 \enspace dt$

$=\displaystyle\frac{1}{4}t^4+C$

$=\displaystyle\frac{1}{4}\sin^4 x+C$

※ $\displaystyle\int f(g(x))g^{\prime}(x)\enspace dx=\displaystyle\int f(u)\enspace du$ の利用

$\displaystyle\int \displaystyle\sin^3 x\cos x\enspace dx=\displaystyle\int \sin^3 x(\sin x)^{\prime}\enspace dx=\displaystyle\frac{1}{4}\sin^4 x+C$

が使えるようになると時間短縮できます！

半角・積和の公式を利用して次数下げ

２倍角の公式

・ $\sin^2x=\displaystyle\frac{1-\cos2x}{2}$

・ $\cos^2x=\displaystyle\frac{1+\cos2x}{2}$

例題②

不定積分

$\displaystyle\int \displaystyle\sin^2 x\enspace dx$ を求めよ．

半角の公式を利用すると

$\displaystyle\int \displaystyle\sin^2 x\enspace dx=\displaystyle\int \displaystyle\displaystyle\frac{1-\cos2x}{2}\enspace dx$

$=\displaystyle\frac{1}{2}\displaystyle\int(1-\cos2x)\enspace dx$

$=\displaystyle\frac{1}{2}\left(x-\displaystyle\frac{1}{2}\sin 2x\right)+C$

$=\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{4}\sin 2x+C$

《積和の公式》

$\begin{align*} \sin\alpha \cos\beta &= \frac{1}{2} \{ \sin(\alpha+\beta) + \sin(\alpha – \beta) \} \\[5pt] \cos\alpha \sin\beta &= \frac{1}{2} \{ \sin(\alpha+\beta) – \sin(\alpha – \beta) \} \\[5pt] \cos\alpha \cos\beta &= \frac{1}{2} \{ \cos(\alpha+\beta) + \cos(\alpha – \beta) \} \\[5pt] \sin\alpha \sin\beta &= – \frac{1}{2} \{ \cos(\alpha+\beta) – \cos(\alpha – \beta) \} \\[5pt] \end{align*}$

例題③

不定積分

$\displaystyle\int \displaystyle\sin 3x\cos 2x\enspace dx$ を求めよ．

積和の公式を利用すると、

$\displaystyle\int \displaystyle\sin 3x\cos 2x\enspace dx=\displaystyle\frac{1}{2}\displaystyle\int(\sin 5x+\sin x) \enspace dx$

$=-\displaystyle\frac{1}{10}\cos 5x-\displaystyle\frac{1}{2}\cos x+C$

半角の公式も積和の公式も、次数を下げることが目的です！

次数が下がると積分しやすい形になると言うことをおさえておきましょう！

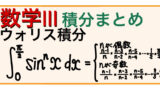
$\displaystyle\int^\frac{\pi}{2}_{0}\sin^nx\enspace dx$ について

$I_{n}=\displaystyle\int^\frac{\pi}{2}_{0} \sin^nx\enspace dx=\displaystyle\int^\frac{\pi}{2}_{0} \cos^nx\enspace dx$

$n$ が偶数のとき

$I_{n}=\displaystyle\frac{n-1}{n}\times\displaystyle\frac{n-3}{n-2}\times\displaystyle\frac{n-5}{n-4}\times\cdots\times\displaystyle\frac{1}{2}\times\displaystyle\frac{\pi}{2}$

$n$ が奇数のとき

$I_{n}=\displaystyle\frac{n-1}{n}\times\displaystyle\frac{n-3}{n-2}\times\displaystyle\frac{n-5}{n-4}\times\cdots\times\displaystyle\frac{2}{3}\times1$

公式の証明については、「【数学Ⅲ】(sinx)^n、(cosx)^nの積分公式・証明・例題演習(ウォリス積分)」

【数学Ⅲ】(sinx)^n、(cosx)^nの積分公式・証明・例題演習(ウォリス積分)

三角関数(sin,cos)のｎ乗の積分公式の証明、例題演習。数学Ⅲ積分。２次試験頻出。ウォリス積分。

例題④〜⑥

④　

$\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x \enspace dx$

⑤　

$\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^5x \enspace dx$

⑥　

$\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x\cos^2x \enspace dx$

④　 $\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x \enspace dx=\displaystyle\frac{3}{4}\times\displaystyle\frac{1}{2}\times\displaystyle\frac{\pi}{2}=\displaystyle\frac{3\pi}{16}$

⑤　 $\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^5x \enspace dx=\displaystyle\frac{4}{5}\times\displaystyle\frac{2}{3}\times1=\displaystyle\frac{8}{15}$

⑥　 $\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x\cos^2x \enspace dx$

$=\displaystyle\int^{\frac{\pi}{2}}_{0}\sin^4x(1-\sin^2x) \enspace dx$

$=\displaystyle\int^{\frac{\pi}{2}}_{0}(\sin^4x-\sin^6x) \enspace dx$

$=\displaystyle\frac{3}{4}\times\displaystyle\frac{1}{2}\times\displaystyle\frac{\pi}{2}-\displaystyle\frac{5}{6}\times\displaystyle\frac{3}{4}\times\displaystyle\frac{1}{2}\times\displaystyle\frac{\pi}{2}=\displaystyle\frac{\pi}{32}$