【問題4】
複素数 \(z\) に関する等式
\(| z + i |+| z – i | = 2\sqrt{2}\) ・・・①
について、次の問に答えよ.
(1) \(z\) が①を満たすとき、\(\overline{z}\) も①を満たすことを示せ.
(2) \(z=x+yi\) が①を満たすとき、\(w=\sqrt{2}x+yi\) は \(| w | = \sqrt{2}\) を満たすことを示せ.
![]()
ここでは、数学Ⅲで学習する複素数平面について、実践問題(入試問題)を使って、ポイント(考え方)まとめをしていきます。
正直に言いますと、教科書をやっただけでは、入試レベルの問題に対応するのは難しいです。
ですから、教科書と入試レベルの橋渡しとして、過去に出題された入試問題を例に、複素数平面においておさえておきたい(入試でよく出る考え方)をまとめていきます。
基本的な考え方をしっかりと身に付け、2次試験で得点源にできるようにしていきましょう!
考え方【Ⅰ】計算処理
①の \(z\) に \(\bar{z}\) を代入した
\(| \overline{z}+1 |+| \overline{z}-i | = 2\sqrt{2}\) を示せばよい.
☞ \(| z | = | \overline{z} |\) の利用
(1) 解答
\(| z+i | = | \overline{z+i} | = | \overline{z}-i |\)
\(| z-i | = | \overline{z-i} | = | \overline{z}+i |\) より
\(| z + i |+| z – i | = | \overline{z}-i |+| \overline{z}+i |\)
したがって、\(| \overline{z}-i |+| \overline{z}+i |=2\sqrt{2}\) を満たすので、\(\overline{z}\) も①を満たす.
(2) 解答
①に \(z=x+yi\) を代入すると、
\(| x+yi+i |+| x+yi-i | = | x+(y+1) i |+| x+(y-1) i | = 2\sqrt{2}\)
\(\sqrt{x^2+(y+1)^2}+\sqrt{x^2+(y-1)^2} = 2\sqrt{2}\)
\(\sqrt{x^2+(y+1)^2} = 2\sqrt{2} – \sqrt{x^2+(y-1)^2}\)
2乗して、
\(x^2+(y+1)^2=8-4\sqrt{2}\sqrt{x^2+(y-1)^2}+x^2+(y-1)^2\)
式を整理して
\(\sqrt{2}\sqrt{x^2+(y-1)^2}=2-y\)
さらに2乗して、
\(2\left\{x^2+(y-1)^2\right\}=(2-y)^2\)
よって、\(2x^2+y^2=2\) ・・・②
\(w=\sqrt{2}x+yi\) のとき
\(| w | = | \sqrt{2}x+yi | = \sqrt{2x^2+y^2}\)
②より
\(| w | = \sqrt{2}\)
考え方【Ⅱ】図形処理
\(| z + i |+| z – i | = 2\sqrt{2}\) ・・・① は、
2点 \(-i\) と \(i\) からの距離の和が \(2\sqrt{2}\)
☞ 楕円
(1) ある方程式(本問では①のこと)において、\(z\) と \(\bar{z}\) をともに満たす
☞ \(z\) と \(\overline{z}\) は実軸に関して対称であるから、
その方程式(本問では①)が実軸に関して対称であることを示せばよい.
(2) \(z=x+yi\) は、「\(z\) の実部を \(\sqrt{2}\) 倍、虚部はそのまま」に変形した図形のことである
別解
(1)、(2)の別解
\(P ( z )\)、\(A ( -i )\)、\(B ( i )\) とおくと、
①は \(AP+BP=2\sqrt{2}\)
つまり \(P ( z )\) は、2点 \(A\)、\(B\) を焦点 とする楕円を表す.
この楕円は、実軸に関して対称なグラフであるから、\(z\) が①を満たすとき、\(\bar{z}\) も①を満たす.
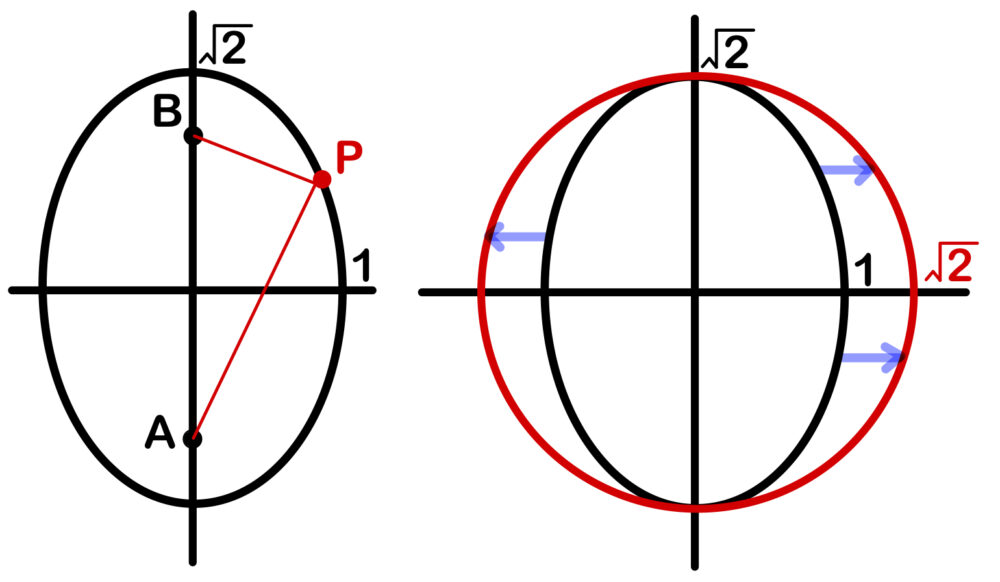
(2) \(z=x+yi\) は、\(z\) の実部を \(\sqrt{2}\) 倍したものであるから、
\(w\) は中心が原点、半径が \(\sqrt{2}\) の円を表す.
つまり、\(| w | = \sqrt{2}\)









コメント