 【オイラー直線】
【オイラー直線】
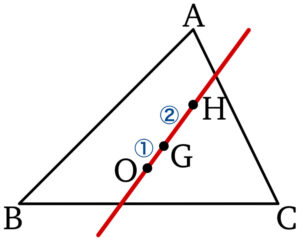
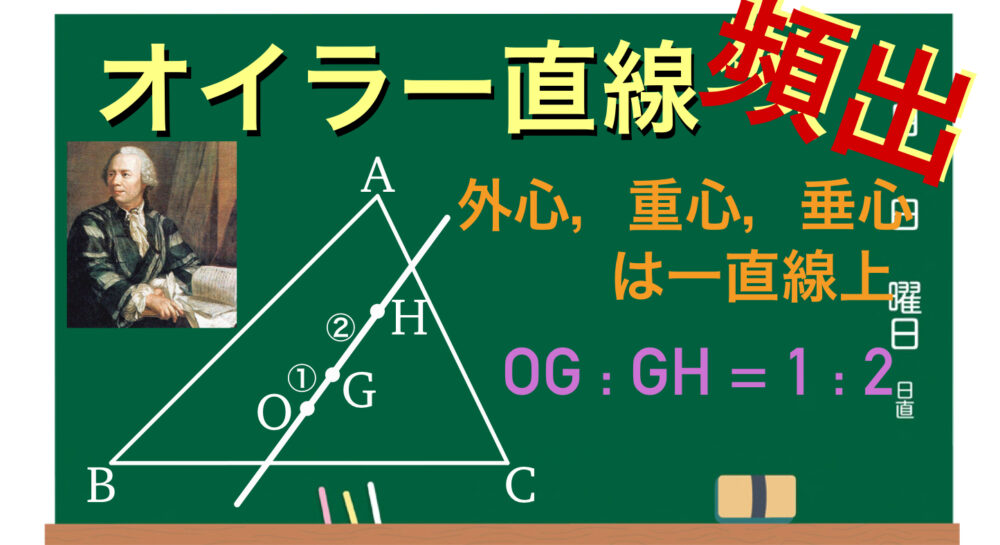
任意の三角形の外心を \(O\) , 重心を \(G\) , 垂心を \(H\) とおくとき,
\(3\) 点 \(O\) , \(G\) , \(H\) は一直線上にある.
また,\(OG:GH=1:2\) を満たす.
とても有名な図形の性質で,様々な証明の仕方があります。
ここでは一番簡単かつ,大学入試でも出題されたことのある形式の,ベクトルを用いた証明を考えてみます。
準備①重心の位置ベクトル
重心( 以下では \(G\) と表す )とは,中線の交点であり,中線を \(2:1\) に内分する点.
(※ 中線とは,各頂点と対辺の中点を結ぶ線分)
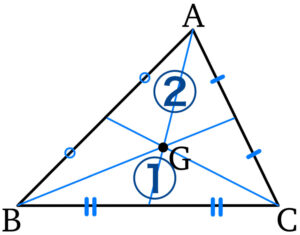 \(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
\(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
参考:始点をAにすると(OをAに変えた)
\(\overrightarrow{AG}=\displaystyle\frac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\)
準備②外心と垂心について
外心を \(O\) , 垂心を \(H\) とするとき
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\)
まずは結果を覚えておきましょう!ちなみに証明問題もよく入試で出題されています!
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\) のとき \(H\) は垂心である証明
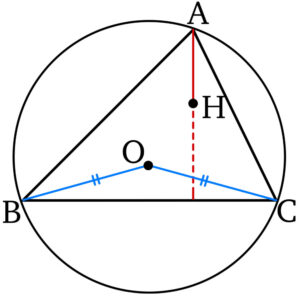 点 \(O\) を外心,
点 \(O\) を外心,
\(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\) ・・・① とおく.
このとき,\(\overrightarrow{AH}=\overrightarrow{OH}-\overrightarrow{OA}\) より
①から,\(\overrightarrow{AH}=\overrightarrow{OB}+\overrightarrow{OC}\)
また,\(\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}\) より
\(\overrightarrow{AH}\cdot\overrightarrow{BC}=(\overrightarrow{OB}+\overrightarrow{OC})(\overrightarrow{OC}-\overrightarrow{OB})=\left|\overrightarrow{OC}\right|^2-\left|\overrightarrow{OB}\right|^2\) ・・・②
点 \(O\) は外心であるから,\(\left|\overrightarrow{OB}\right|=\left|\overrightarrow{OC}\right|\) であるから,②より
\(\overrightarrow{AH}\cdot\overrightarrow{BC}=0\)
したがって,\(\overrightarrow{AH} \perp \overrightarrow{BC}\)
同様に,\(\overrightarrow{BH} \perp \overrightarrow{CA}\) ,\(\overrightarrow{CH} \perp \overrightarrow{AB}\) となり,点 \(H\) は垂心となる.
\(3\) 点 \(O\) , \(G\) , \(H\) が一直線上にある証明
上の準備①,準備②より
 \(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
\(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
かつ \(\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\) であるから
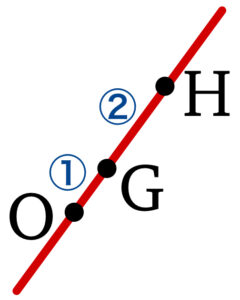
\(\overrightarrow{OH}=3\overrightarrow{OG}\) より \(3\) 点 \(O\) , \(G\) , \(H\) は一直線上にある.
また,\(OG:GH=1:2\) を満たす.







コメント
垂心であることの証明の⓵から、のやつOHじゃなくてAHだと思います
ご指摘ありがとうございます。
間違いを訂正させていただきました。
これからもよろしくお願いいたします。