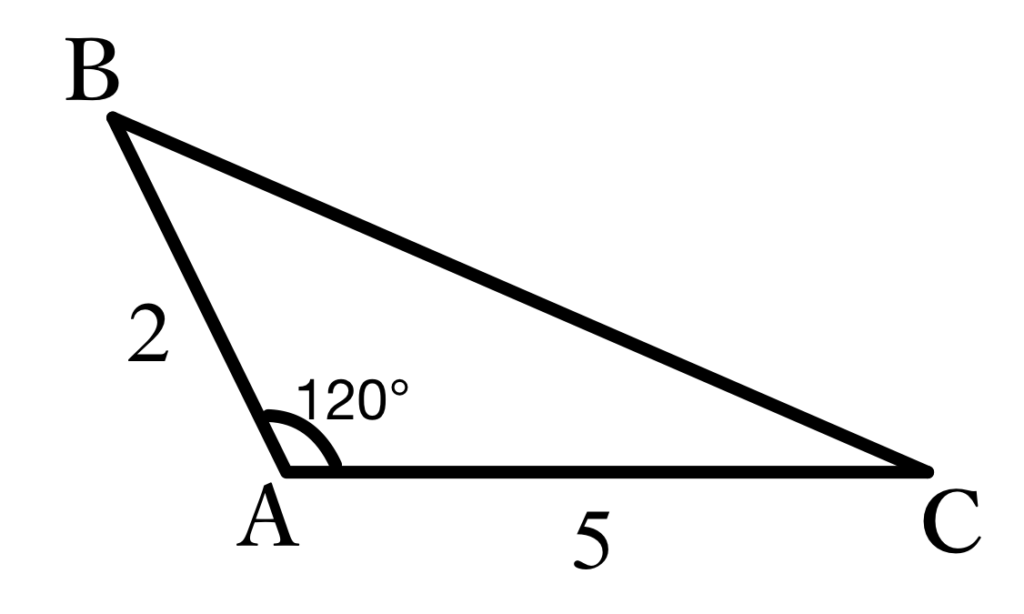
平面図形へのアプローチ
おそらく多くの人が余弦定理を用いて計算を行ったのではないでしょうか?もちろん正解です!
ただここでお話ししたいことは、解けたかどうかではありません。(もちろん解けて欲しいですが・・・)
そもそも、どうしてこの問題を見て『幾何(三角比)』の問題だと思ったのでしょうか?
ベクトルや座標は頭の中に浮かびましたか??
ベクトルや座標を考慮した上で、幾何的に解くのが一番良いと判断したのであれば何も言うことはありません。
幾何の分野であると決めつけてしまったことに問題があります。
平面図形の問題
👉3つのアプローチ!
①幾何(三角比・合同・相似など)
②座標
③ベクトル
(数Ⅲを履修している人は④複素平面 ⑤極座標など)
それぞれの解法どの解法が良いとか悪いと言うことではありません。
まずはどれでも良いので解けることが前提。その上で、レベルアップをしたいのであればすべての解法が思いつくようになって欲しい!
なぜ3つのアプローチ?
幾何の問題は差がつきやすい(合否を分ける問題になりやすい)
2次試験の問題は、1題あたり30~50点前後。
例えば相似に気がつけなかったら・・・。それだけで50点が・・・。
そのようなときに、幾何的なアプローチは出来ずとも、座標で考えてみようと思えることが大切。
それでもダメだったらベクトルは?と次から次へと手が出せるかどうかがとても重要。
3つやってみてどれもダメならそれは仕方ない。でも3つのうち、少しでも部分点がもらえる可能性があることが記述できそうであれば、僅かな点数ながらも0点は回避できます。
大学入試は全分野から出題される
学校では分野ごとに教科書で学習し、分野ごとに問題集を使って演習を行います。
もちろん習いたての時はしっかりと分野ごとに学習することが大切です。しかしそれだけでは2次試験の問題ではなかなか太刀打ちが出来ない問題も多々あります。
ちなみに2次試験の問題は、大学や学部にもよりますが、大問で3~6題であることが多いと思います。
大学によっては○○の分野は出題されないなど一部例外はありますが、できる限り全分野から出題したいと考えていると知り合いの某有名大学の教授はおっしゃっていました。
つまり、1つの大問に様々な分野を絡めて出題されると言うこと。だからこそ、見た目だけで○○の分野の問題と決めつけてかかることは、解法パターンを狭めてしまうことになるので危険。
練習でできないことは本番では絶対にできない
これは勉強に限ったことではありませんが、今回例に示したような簡単な問題でさえも複数の解答がパッと頭の中に浮かばなければ(浮かぶような練習をしていなければ)、入試本番では絶対にできるようになりません。
その為にあえて今回は易しい問題を例にとって話をしています。
だからこそ,しっかりと分野ごとで頑張って勉強してきたものを、分野問わずに様々な問題を用いて様々な解法で思考していく練習が必要です。そのような練習は学校の授業ではなかなかやってくれませんし,自分一人では難しいのかと思います。
だからこそこのブログを通して、様々な考え方、問題のアプローチの仕方、また教科書では扱わないが入試では頻出テーマなど、プラスαな情報をお届けしたいと思います。さらに、受験に必要な情報も提供出来たらよいなとも思っています。
それでは改めて,3つの解法を考えてみてください。
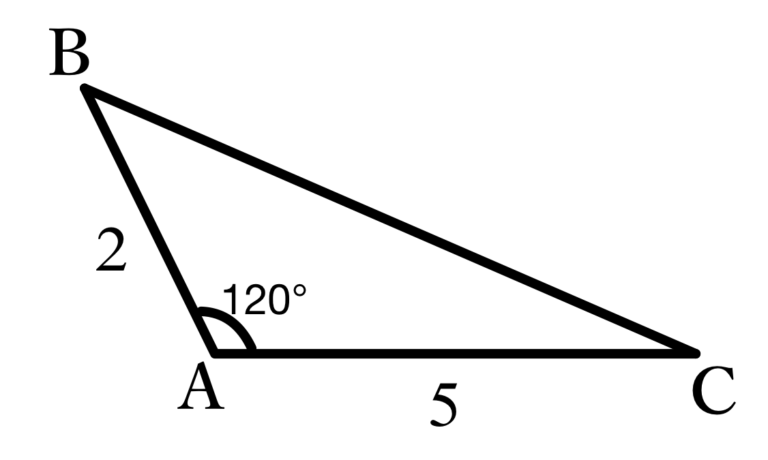
解法① 幾何
これはほとんどの人が最初に思いつく解法でしょう。
余弦定理より
\(BC^2=AB^2+AC^2-2\times{AB}\times{AC}\times\cos{A}\)
\(BC^2=2^2+5^2-2\times2\times5\times\cos{120\text{°}}\)
\(BC^2=39\\BC=\sqrt{39}\)
解法② 座標
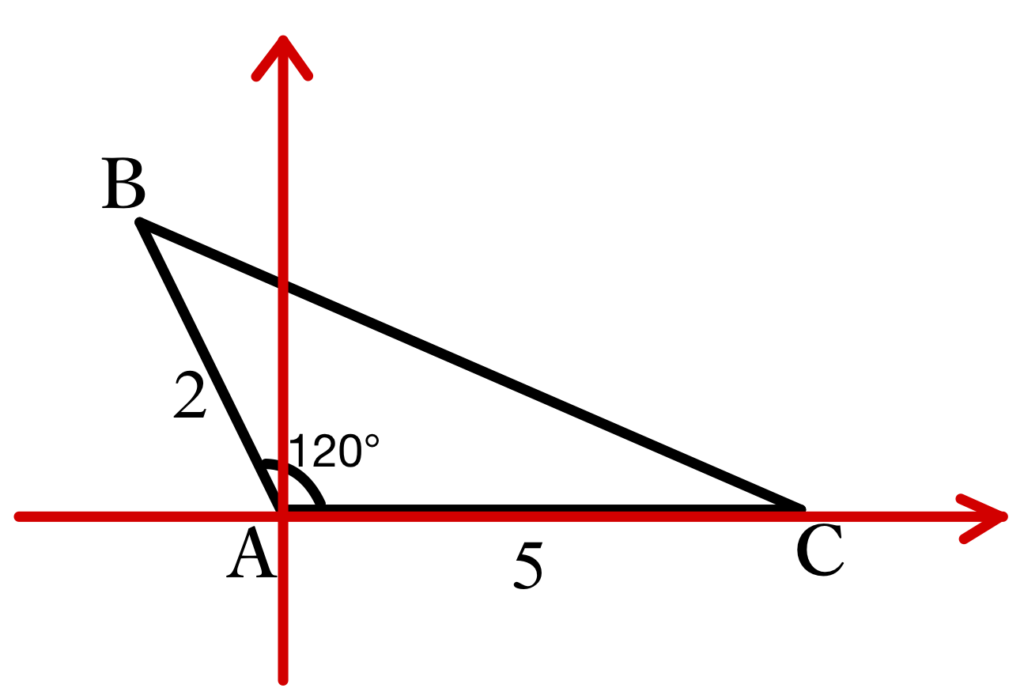
上図のように,点Aを原点,ACがx軸上にくるように軸をとる。
このとき,\(A(0,0),B (-1 , \sqrt{3}) , C ( 5 , 0 ) \)
よって2点間の距離の公式を用いて,
\(BC=\sqrt{(5-(-1))^2+\sqrt{3}^2}=\sqrt{39}\)
解法③ ベクトル
\(|\overrightarrow{BC}|=|\overrightarrow{AC}-\overrightarrow{AB}|\)
両辺を2乗して(👈ベクトルで大きさに関する問題は2乗するのが定石!)
\(|\overrightarrow{BC}|^2=|\overrightarrow{AC}|^2-2\overrightarrow{AC}\cdot\overrightarrow{AB}+|\overrightarrow{AB}|^2\)
\(|\overrightarrow{BC}|^2=|\overrightarrow{AC}|^2-2|\overrightarrow{AC}||\overrightarrow{AB}|\cos{A}+|\overrightarrow{AB}|^2\)
\(|\overrightarrow{BC}|^2=5^2-2\times5\times 2\times \cos{120\text{°}}+2^2\)
\(|\overrightarrow{BC}|^2=39\)
\(|\overrightarrow{BC}|=\sqrt{39}\)
まとめ
どれが良いとか悪いということが目的ではありません。
簡単な問題で3つ考える習慣を身につけ,いざ本番でも使いこなせるように練習していきましょう!
3つでアプローチしても解けなければ仕方ありませんが,大切なのは解けなくてもいいから少しでも部分点を取りにいくこと!
結果としてそれが合否の差を分けます。合格に一歩でも近づきましょう!!
最後まで読んでいただき【問題の解答のルートの中の数字】






コメント