【2021数学ⅠA(第1日程)】第1問[1](2次方程式)
(1)問題と解答・解説《ア〜ウ》

(1)解答・解説《ア〜ウ》
\(c=1\) のとき①の左辺は
\(2x^2+x-10=\)\((2x+5)(x-2)\) ・・・《ア〜ウ》
よって①の解は,\(x=-\displaystyle\frac{5}{2} , 2\)
(2)問題と解答・解説《エ〜シ》
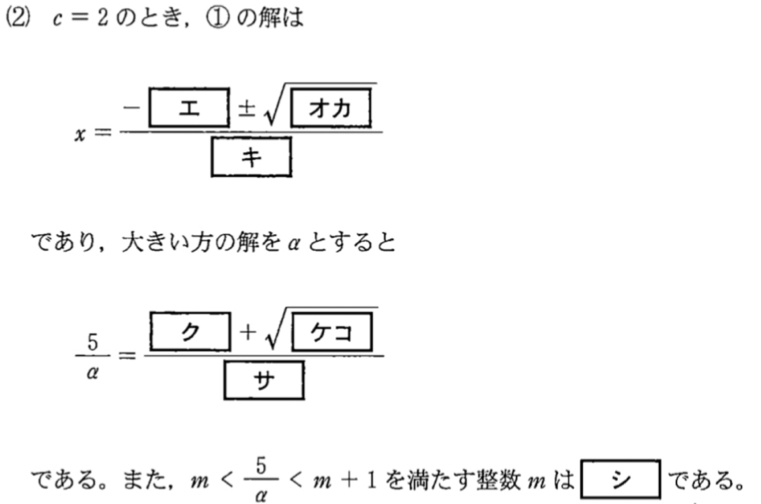
(2)解答・解説《エ〜シ》
\(c=2\) のとき①は,
\(2x^2+5x-5=0\)
\(x=\displaystyle\frac{-5\pm\sqrt{65}}{4}\) ・・・《エ〜キ》
よって大きい方の解 \(\alpha\) は,
\(\alpha=\displaystyle\frac{-5+\sqrt{65}}{4}\) であるから,
\(\displaystyle\frac{5}{\alpha}=5\times \displaystyle\frac{4}{-5+\sqrt{65}}\)
\(=\displaystyle\frac{20(\sqrt{65}+5)}{(\sqrt{65}-5)(\sqrt{65}+5)}\)
\(=\displaystyle\frac{5+\sqrt{65}}{2}\) ・・・《ク〜サ》
\(8=\sqrt{64}<\sqrt{65}<\sqrt{81}=9\) より
\(\displaystyle\frac{5+8}{2}<\displaystyle\frac{5+\sqrt{65}}{2}<\displaystyle\frac{5+9}{2}\)
\(6.5<\displaystyle\frac{5}{\alpha}<7\) より \(m=6\) ・・・《シ》
(3)問題と解答・解説《ス》

(3)解答・解説《ス》
\(2x^2+(4c-3)x+2c^2-c-11=0\) ・・・① の解は
\(x=\displaystyle\frac{-(4c-3)\pm\sqrt{(4c-3)^2-4\times 2\times (2c^2-c-11)}}{4}\)
式を整理すると,\(x=\displaystyle\frac{-4c+3\pm\sqrt{-16c+97}}{4}\)
この \(2\) 解がともに有理数となるのは, \(-16c+97\) ( ルートの中 ) が平方数になるときである.
ここで, \(-16c+97>0\) であるから
\(c<\displaystyle\frac{97}{16}\)
\(c\) は正の整数であるから,\(c=1,2,3,4,5,6\)
この中で \(-16c+97\) が平方数となるのは
・\(c=1\) のとき \(-16c+97=81=9^2\)
・\(c=3\) のとき \(-16c+97=49=7^2\)
・\(c=6\) のとき \(-16c+97=1=1^2\)
の \(3\) 個 ・・・《ス》









コメント