【2021数学ⅡB(第1日程):第5問ベクトル】
(1)問題と解答・解説
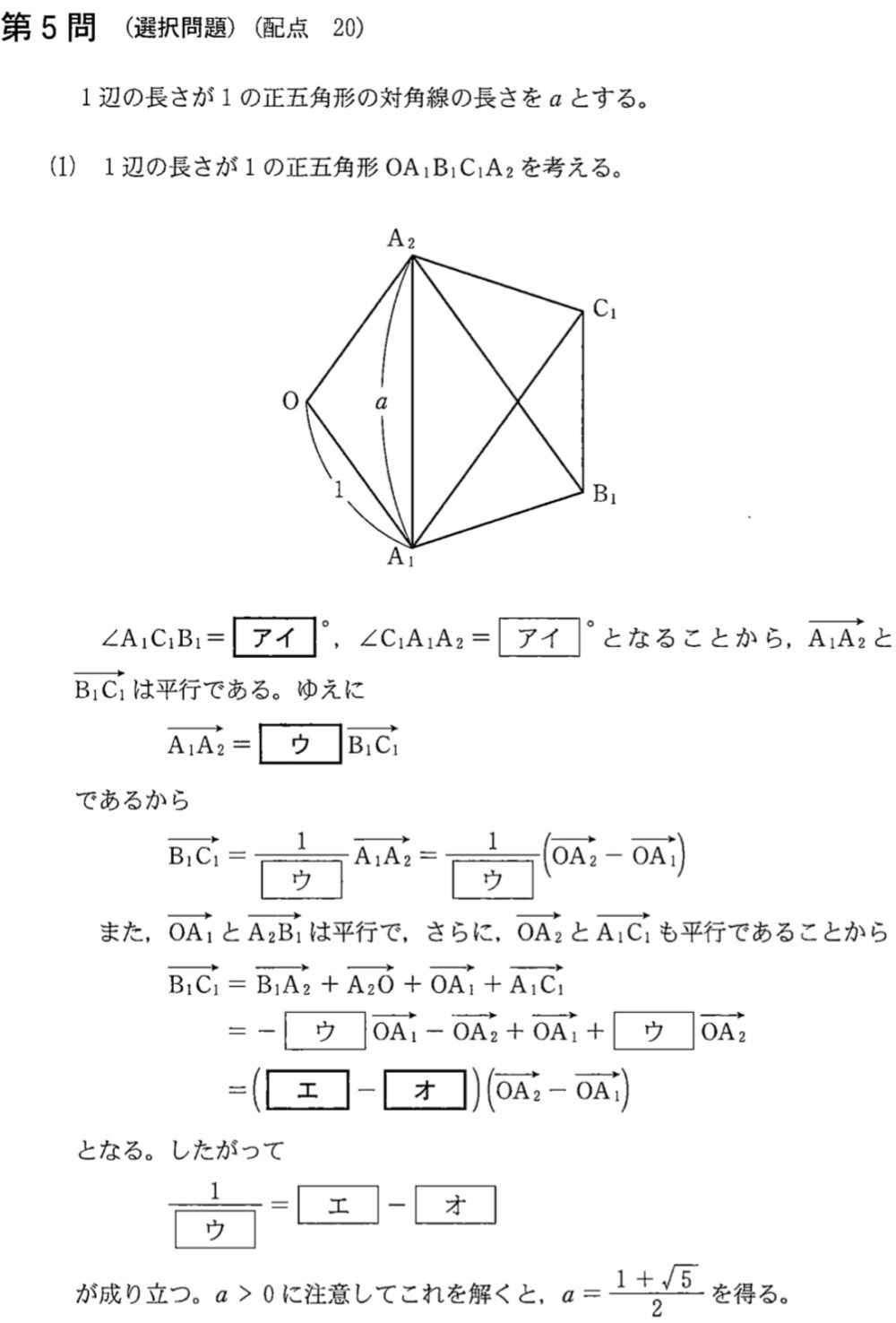
(1)解答・解説《ア〜オ》
正五角形の \(1\) つの内角の大きさは,
\(\displaystyle\frac{180°\times (5-2)}{5}=108°\)
よって,\(\angle A_{1}C_{1}B_{1}=\displaystyle\frac{108°}{3}=\)\(36°\) ・・・《アイ》
\(\angle C_{1}A_{1}A_{2}=36°\) となり錯角が等しいので
\(\overrightarrow{A_{1}A_{2}}\) / / \(\overrightarrow{B_{1}C_{1}}\)
\(\left|\overrightarrow{A_{1}A_{2}}\right|=a\) , \(\left|\overrightarrow{B_{1}C_{1}}\right|=1\) より
\(\overrightarrow{A_{1}A_{2}}=a\overrightarrow{B_{1}C_{1}}\) ・・・《ウ》
よって,\(\overrightarrow{B_{1}C_{1}}=\displaystyle\frac{1}{a}\overrightarrow{A_{1}A_{2}}=\displaystyle\frac{1}{a}\left(\overrightarrow{OA_{2}}-\overrightarrow{OA_{1}}\right)\)
また,\(\overrightarrow{OA_{1}}\) / / \(\overrightarrow{A_{2}B_{1}}\),\(\overrightarrow{OA_{2}}\) / / \(\overrightarrow{A_{1}C_{1}}\) より
\(\overrightarrow{B_{1}C_{1}}=\overrightarrow{B_{1}A_{2}}+\overrightarrow{A_{2}O}+\overrightarrow{OA_{1}}+\overrightarrow{A_{1}C_{1}}\)
\(=-a\overrightarrow{OA_{1}}-\overrightarrow{OA_{2}}+\overrightarrow{OA_{1}}+a\overrightarrow{OA_{2}}\)
\(=(1-a)\left(\overrightarrow{OA_{2}}-\overrightarrow{OA_{1}}\right)\) ・・・《エオ》
したがって,\(\displaystyle\frac{1}{a}=1-a\)
\(a^2-a-1=0\)
\(a>0\) に注意してこれを解くと \(a=\displaystyle\frac{1+\sqrt{5}}{2}\)
(2)問題と解答・解説
(2)−①解答・解説《カ〜サ》
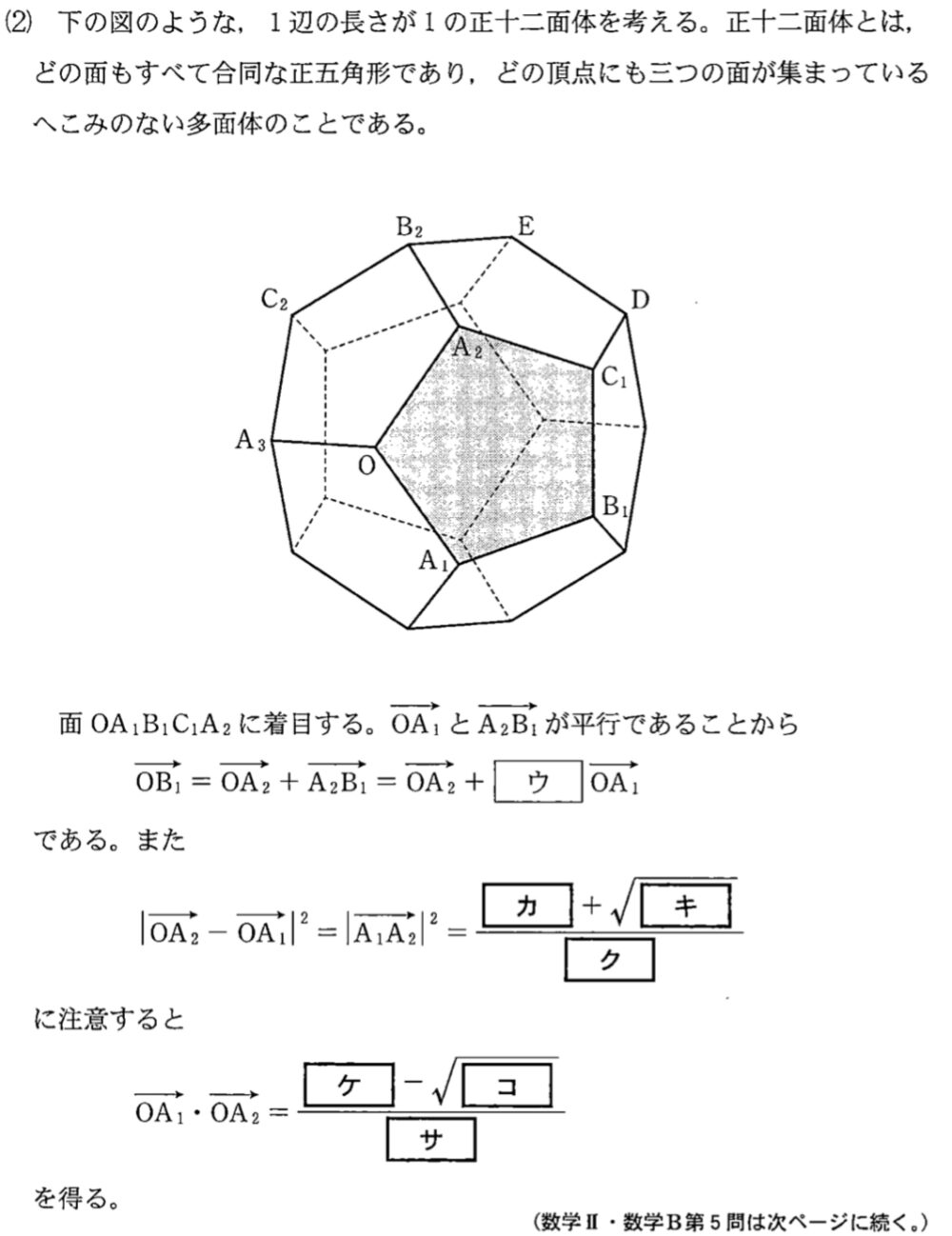
\(\overrightarrow{OB_{1}}=\overrightarrow{OA_{1}}+\overrightarrow{A_{2}B_{1}}=\overrightarrow{OA_{2}}+a\overrightarrow{OA_{1}}\) ・・・①
また,\(\left|\overrightarrow{OA_{2}}-\overrightarrow{OA_{1}}\right|^2=\left|\overrightarrow{A_{1}A_{2}}\right|^2=a^2\)
(1) より \(a^2-a-1=0\)
\(a^2=a+1=\displaystyle\frac{1+\sqrt{5}}{2}+1=\)\(\displaystyle\frac{3+\sqrt{5}}{2}\) ・・・《カキク》
\(\left|\overrightarrow{OA_{2}}-\overrightarrow{OA_{1}}\right|^2=\left|\overrightarrow{OA_{2}}\right|^2-2\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}+\left|\overrightarrow{OA_{1}}\right|^2=2-2\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}\) であるから
\(\displaystyle\frac{3+\sqrt{5}}{2}=2-2\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}\)
よって,\(\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}=\displaystyle\frac{1-\sqrt{5}}{4}\) ・・・《ケコサ》
(2)−②解答・解説《シス》
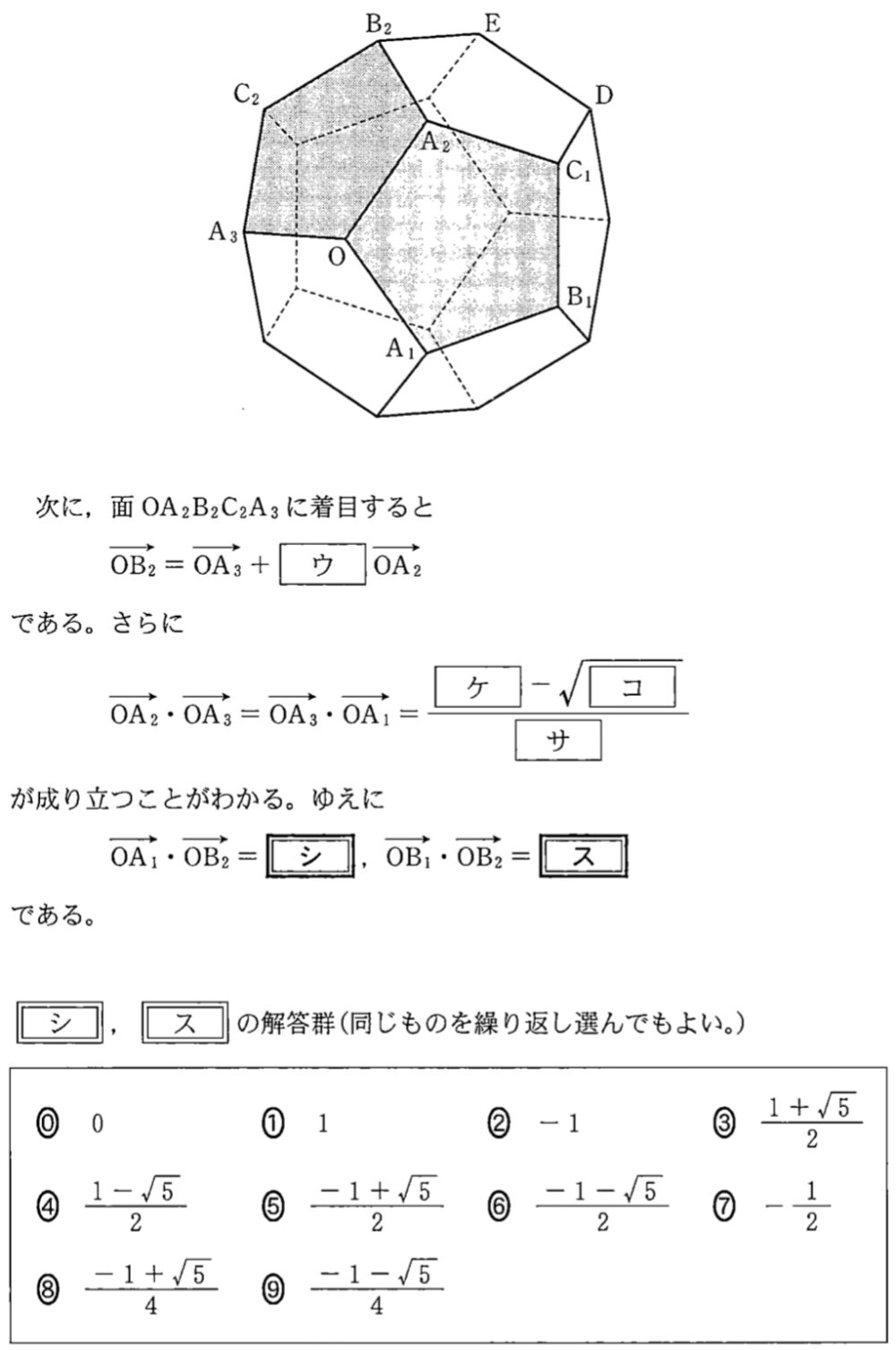
次に,面 \(OA_{2}B_{2}C_{2}A_{3}\) に着目すると
\(\overrightarrow{OB_{2}}=\overrightarrow{OA_{3}}+a\overrightarrow{OA_{2}}\)
さらに,各面はすべて合同な正五角形であるから,
\(\overrightarrow{OA_{2}}\cdot\overrightarrow{OA_{3}}=\overrightarrow{OA_{3}}\cdot\overrightarrow{OA_{1}}=\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}=\displaystyle\frac{1-\sqrt{5}}{4}\)
が成り立つので,
\(\overrightarrow{OA_{1}}\cdot\overrightarrow{OB_{2}}=\overrightarrow{OA_{1}\cdot\left(\overrightarrow{OA_{3}}+a\overrightarrow{OA_{2}}\right)}\)
\(=\overrightarrow{OA_{3}}\cdot\overrightarrow{OA_{1}}+a\overrightarrow{OA_{1}}\cdot\overrightarrow{OA_{2}}\)
\(=\displaystyle\frac{1-\sqrt{5}}{4}(1+a)\)
\(=\displaystyle\frac{-1-\sqrt{5}}{4}\) ・・・《シ:⑨》
さらに,
\(\overrightarrow{OB_{1}}\cdot\overrightarrow{OB_{2}}=\left(\overrightarrow{OA_{2}}+a\overrightarrow{OA_{1}}\right)\cdot\left(\overrightarrow{OA_{3}}+a\overrightarrow{OA_{2}}\right)\)
これを展開して計算すると,\(\overrightarrow{OB_{1}}\cdot\overrightarrow{OB_{2}}=0\) ・・・《ス:⓪》
(2)−③解答・解説《セ》
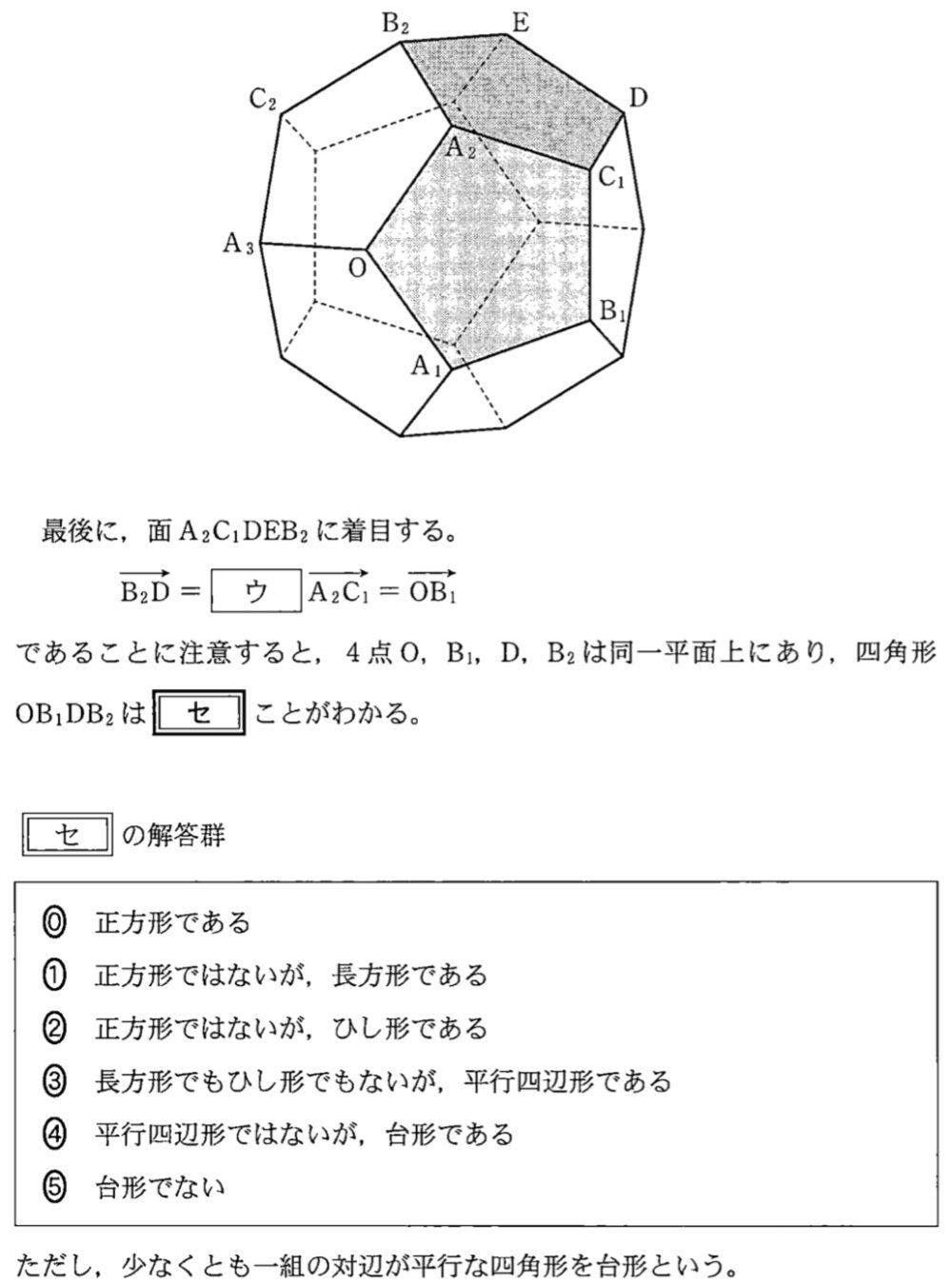
最後に,\(A_{2}C_{1}DEB_{2}\) に着目すると,
\(\overrightarrow{B_{2}D}=a\overrightarrow{A_{2}C_{1}}=\overrightarrow{OB_{1}}\)
であることに注意すると \(4\) 点 \(O\) , \(B_{1}\) , \(D\) , \(B_{2}\) は同一平面上にある.
また,\(OB_{2}\) , \(B_{1}D\) , \(OB_{1}\) , \(B_{2}D\) はすべて合同な正五角形の対角線であるから,
\(OB_{2}=B_{1}D=OB_{1}=B_{2}D=a\)
さらに,《ス》の結果から \(\overrightarrow{OB_{1}}\perp\overrightarrow{OB_{2}}\) であるから,
四角形 \(OB_{1}DB_{2}\) は 「 ⓪正方形である 」・・・《セ》










コメント