【2013東京大学】
\(\triangle ABC\) において \(\angle BAC=90°\) , \(\left|\overrightarrow{AB}\right|=1\) , \(\left|\overrightarrow{AC}\right|=\sqrt{3}\) とする．\(\triangle ABC\) の内部の点 \(P\) が
\(\displaystyle\frac{\overrightarrow{PA}}{\left|\overrightarrow{PA}\right|}+\displaystyle\frac{\overrightarrow{PB}}{\left|\overrightarrow{PB}\right|}+\displaystyle\frac{\overrightarrow{PC}}{\left|\overrightarrow{PC}\right|}=\overrightarrow{0}\)
を満たすとする．
(１) \(\angle APB\) , \(\angle APC\) を求めよ．
(２) \(\left|\overrightarrow{PA}\right|\) , \(\left|\overrightarrow{PB}\right|\) , \(\left|\overrightarrow{PC}\right|\) を求めよ．
考え方・ヒント
重心の位置ベクトル
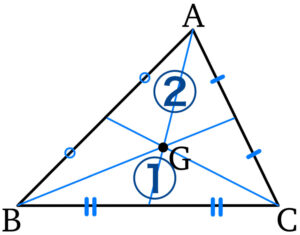\(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)
参考：始点をAにすると(OをAに変えた)
\(\overrightarrow{AG}=\displaystyle\frac{\overrightarrow{AB}+\overrightarrow{AC}}{3}\)
単位ベクトルについて
大きさが \(1\) であるベクトルのことを単位ベクトルという．
ある \(\overrightarrow{a}\) (ただし \(\overrightarrow{0} \)ではない ) の単位ベクトルは，\(\displaystyle\frac{\overrightarrow{a}}{ \left|\overrightarrow{a}\right|} \) と表せる．
平面図形は３つの方針を考える！
パターン問題を除き、次の原則３つを考える
- 幾何
- 座標
- ベクトル
※数学Ⅲまで学習している人は、４．複素数平面，５．極座標 などもあります！
基本的な問題で、上のPointについてで紹介しています．
【差がつく考え方】平面図形の３つのアプローチ！(幾何・座標・ベクトル)ご参考に！
本問では様々な解法が考えられますが，ここでは「１．幾何」を利用した解法を紹介します！
解答
(１)
\(\displaystyle\frac{\overrightarrow{PA}}{\left|\overrightarrow{PA}\right|}=\overrightarrow{PX}\) , \(\displaystyle\frac{\overrightarrow{PB}}{\left|\overrightarrow{PB}\right|}=\overrightarrow{PY}\) , \(\displaystyle\frac{\overrightarrow{PC}}{\left|\overrightarrow{PC}\right|}=\overrightarrow{PZ}\)
となる点をそれぞれ \(X\) , \(Y\) , \(Z\) とおく.
条件より，\(\overrightarrow{PX}+\overrightarrow{PY}+\overrightarrow{PZ}=\overrightarrow{0}\) より
\(\displaystyle\frac{1}{3}\left(\overrightarrow{PX}+\overrightarrow{PY}+\overrightarrow{PZ}\right)=\overrightarrow{0}=\overrightarrow{PP}\) なので
点 \(P\) は \(\triangle XYZ\) の重心 ・・・① となる．
また，\(\left|\overrightarrow{PX}\right|\) , \(\left|\overrightarrow{PY}\right|\) , \(\left|\overrightarrow{PZ}\right|=1\) より，
点 \(P\) は \(\triangle XYZ\) の外心 ・・・② となる．
①，②より，重心と外心が一致するので，\(\triangle XYZ\) は正三角形となる．
したがって，\(\angle APB=\angle APC=120°\)
(２)
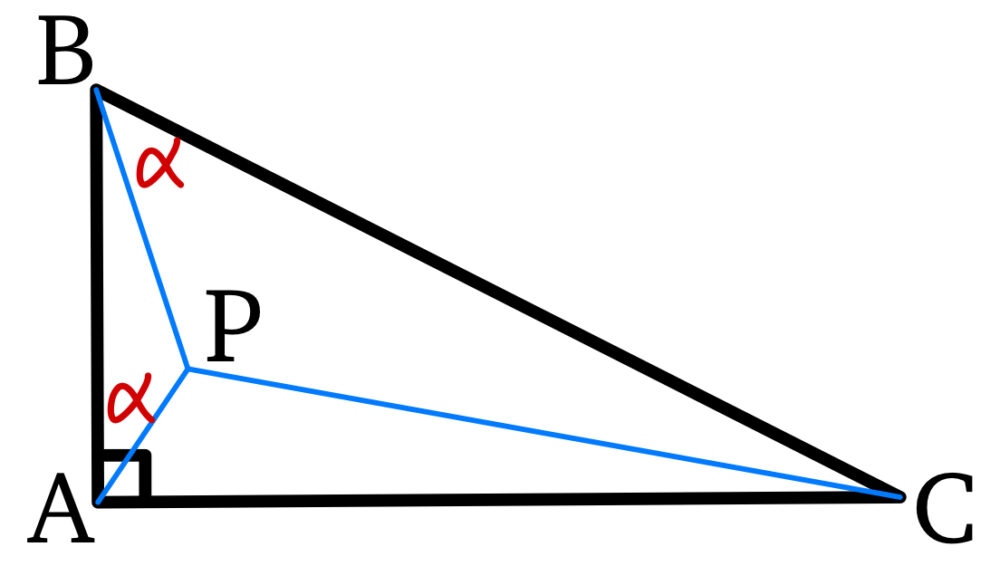
\(\angle BAC=90°\) , \(AB=1\) , \(AC=\sqrt{3}\) より，\(BC=2\) , \(\angle ABC=60°\)
ここで \(\angle PAB=\alpha\) とおく．
\(\angle ABP=180°-(\alpha+120°)=60°-\alpha\)
\(\angle PBC=\angle ABC-\angle ABP=60°-(60°-\alpha)=\alpha\)
よって，\(\angle PAB=\angle PBC\) ・・・③
また(１)より \(\angle APB=\angle BPC=120°\) ・・・④
③，④より \(\triangle PAB\text{∽}\triangle PBC\)
\(PA=x\) とおくと
\(PA : AB=PB : BC\) より
\(x : 1=PB : 2\) \(\iff\) \(PB=2x\)
また，\(AB : PB=BC : PC\) より
\(1 : 2x=2 : PC\) \(\iff\) \(PC=4x\)
\(\triangle PAB\) で余弦定理より
\(x^2+(2x)^2-2\cdot x\cdot 2x\cdot\cos 120°=1^2\)
\(x^2=\displaystyle\frac{1}{7}\)
\(x>0\) より \(x=\displaystyle\frac{\sqrt{7}}{7}\)
したがって，
\(PA=\displaystyle\frac{\sqrt{7}}{7}\) , \(PB=\displaystyle\frac{2\sqrt{7}}{7}\) , \(PC=\displaystyle\frac{4\sqrt{7}}{7}\)
コメント