【2021数学ⅡB(第２日程)】第１問[１](指数・対数関数)

(１)問題と解答・解説《ア〜オ》

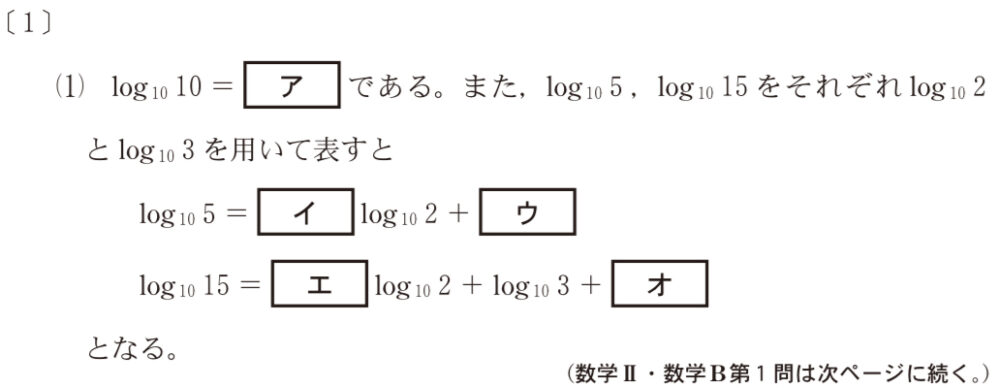
$\log_{10}{10}=1$ ・・・《ア》 である．

また， $\log_{10}{5}=\log_{10}{\displaystyle\frac{10}{2}}=\log_{10}{10}-\log_{10}{2}$ より

$\log_{10}{5}=-\log_{10}{2}+1$ ・・・《イウ》

$\log_{10}{15}=\log_{10}{3\times 5}=\log_{10}{3}+\log_{10}{5}=\log_{10}{3}+\left(-\log_{10}{2}+1\right)$

よって， $\log_{10}{15}=-\log_{10}{2}+\log_{10}{3}+1$ ・・・《エオ》

常用対数における桁数問題、最高位の数字に関する問題は頻出の有名問題です！

$\log_{10}{15^{20}}=20\times \log_{10}{15}=20(-\log_{10}{2}+\log_{10}{3}+1)$

$\log_{10}{2}=0.3010$ ， $\log_{10}{3}=0.4771$ を代入して計算すると

$\log_{10}{15^{20}}=23.522$

\(23<\log_{10}{15^{20}}<\23+1) ・・・《カキ》

を満たす．よって， $15^{20}$ は $24$ 桁・・・《クケ》

$\log_{10}{15^{20}}$ の小数部分は

$\log_{10}{15^{20}}-23=0.522$ であり，

$\log_{10}{3}=0.4771$ ， $\log_{10}{4}=2\times \log_{10}{2}=0.6020$ なので

$\log_{10}{3}<\log_{10}{15^{20}}-23<\log_{10}{4}$ ・・・《コ》が成立

しがたって，

$23+\log_{10}{3}<\log_{10}{15^{20}}<23+\log_{10}{4}$

$\log_{10}{3\times 10^{23}}<\log_{10}{15^{20}}<\log_{10}{4\times 10^{23}}$

$3\times 10^{23}<15^{20}<4\times 10^{23}$ であるから，

$15^{20}$ の最高位の数字は $3$ ・・・《サ》