例題(※ただ答えが求められることが目的ではありません)

実際に解かなくても良いので、最初に何をするか頭の中でイメージしてください。
多くの方がこの問題は解けると思います。
参考として模範解答を載せておきます。
模範解答

しっかり解けていましたか?
それではここからが本題です。
質問です。
解答の1行目・・・なぜ①を代入して良いのか説明できますか?
これがしっかりと説明できないということは、「媒介変数表示」を使いこなせていないということになります。下記の説明をみて、しっかりと媒介変数について学習し、発展的な問題で応用できる力を身につけていきましょう!
媒介変数(パラメータ)表示とは?
媒介変数表示とは、変数 x、y を別の文字 t やθ などを用いて表すことです。
そもそも、直線や曲線は点の集まりです。その点の代表選手を考えようと言った発想です。
少し具体的に考えてみましょう。
$$2x+y=5 ・・・①$$
①をみたす値について考えてみると
$$(x,y)=(0,5) \Rightarrow x^2+y^2=0^2+5^2=25$$
$$(x,y)=(1,3) \Rightarrow x^2+y^2=1^2+3^2=10$$
$$(x,y)=(2,1) \Rightarrow x^2+y^2=2^2+1^2=5$$
$$(x,y)=\left(\frac{ 1 }{ 2 },4\right) \Rightarrow x^2+y^2=\left(\frac{ 1 }{ 2 }\right)^2+4^2=\frac{ 65 }{ 4 }$$
①を満たすありとあらゆる点を代入し、その中から最小になる値を探そうということをしています。
しかし①を満たす点を全て調べるのはとっても大変(というよりは無理・・・)
そこで
$$\begin{cases}x=t\\y=-2t+5 \end{cases}$$
このように①を満たす任意の点を考え代入し、
$$x^2+y^2=t^2+(-2t+5)^2$$
を考えていくわけです。あとは最初に書いた模範解答通りになります。
つまり結果的に①をただ代入したような形になっただけということです。
円の媒介変数
例題では直線の媒介変数について扱いました。
大学受験で最もよく出題されている媒介変数としては、「円の媒介変数表示」が有名です。
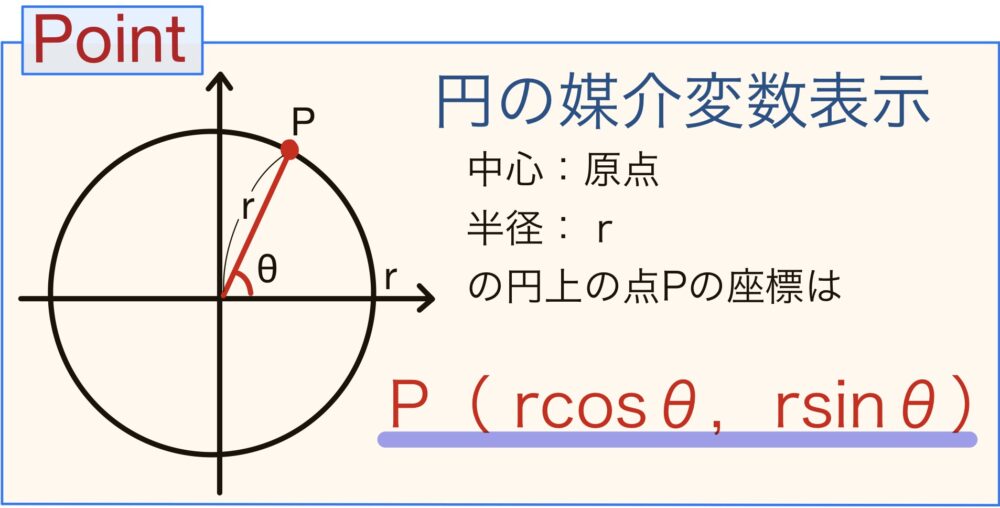
円の媒介変数表示は絶対に使いこなせるようにしましょう。
他にも数学Ⅲを学習する人は、楕円、双曲線、サイクロイドなど、有名な媒介変数表示もあります。







コメント