【2022大阪医科薬科大学・看護・[１]】
解答・解説
(１) 対称式の利用
覚えておきたい対称式の公式
・\(a^2+b^2=(a+b)^2-2ab\)
・\(a^3+b^3=(a+b)^3-3ab(a+b)\)
・\(a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ca)\)
\(A^2+B^2=(A+B)^2-2AB\) ・・・①
①において，\(A=a^2\)，\(B=\displaystyle\frac{1}{a^2}\) とすると
\(a^4+\displaystyle\frac{1}{a^4}=\left(a^2+\displaystyle\frac{1}{a^2}\right)^2-2\cdot a^2\cdot \displaystyle\frac{1}{a^2}=\left(a^2+\displaystyle\frac{1}{a^2}\right)^2-2\)
\(a^4+\displaystyle\frac{1}{a^4}=34\) より
\(\left(a^2+\displaystyle\frac{1}{a^2}\right)^2-2=34\)
\(\left(a^2+\displaystyle\frac{1}{a^2}\right)^2=36\)
\(a^2+\displaystyle\frac{1}{a^2}>0\) より \(a^2+\displaystyle\frac{1}{a^2}=6\)
また①において，\(A=a\)，\(B=\displaystyle\frac{1}{a}\) とすると
\(a^2+\displaystyle\frac{1}{a^2}=\left(a+\displaystyle\frac{1}{a}\right)^2-2\cdot a\cdot \displaystyle\frac{1}{a}=\left(a+\displaystyle\frac{1}{a}\right)^2-2=6\)
よって \(\left(a+\displaystyle\frac{1}{a}\right)^2=8\)
\(a>0\) より \(a+\displaystyle\frac{1}{a}>0\) であるから，
\(a+\displaystyle\frac{1}{a}=2\sqrt{2}\) ・・・( d )
(２) 相関係数
散布図を利用した解答
散布図に \(8\) 個のデータを書き込むと以下のようになる．
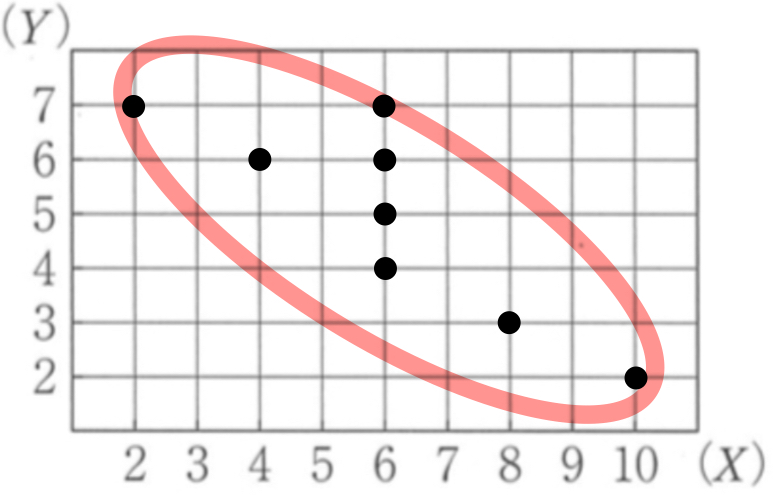
負の相関をもつことがわかるので，相関係数 \(r\) は，\(-1≦r<0\) ・・・( a )
散布図を利用することで，ざっくりした相関係数の値は見当がつきます。
しかし具体的な値までは分かりませんので，必要に応じて計算もできるようにしておきましょう！
参考として下記で，相関係数の計算も与えておきます。
相関係数の計算による解答
平均値，中央値，最頻値，分散，標準偏差，共分散、相関係数など，公式が不安な方はしっかりと確認はしておきましょう！
【2021聖マリアンナ医科大学】データの分析と整数問題｜分散の最大・最小
をご参考に！
\(\overline{X}=\displaystyle\frac{1}{8}(6+8+6+10+4+6+2+6)=6\)
\(\overline{Y}=\displaystyle\frac{1}{8}(4+3+5+2+6+7+7+6)=5\)
データ \(X\)，\(Y\) の分散をそれぞれ \(S^2_{x}\)，\(S^2_{Y}\) とすると
\(S^2_{X}=\displaystyle\frac{1}{8}\left\{(6-6)^2+(8-6)^2+(6-6)^2+(10-6)^2\\+(4-6)^2+(6-6)^2+(2-6)^2+(6-6)^2\right\}=5\)
\(S^2_{Y}=\displaystyle\frac{1}{8}\left\{(4-5)^2+(3-5)^2+(5-5)^2+(2-5)^2\\+(6-5)^2+(7-5)^2+(7-5)^2+(6-5)^2\right\}=3\)
よってデータ \(X\)，\(Y\) の標準偏差は \(S_{X}=\sqrt{5}\)，\(S_{Y}=\sqrt{3}\)
またデータ \(X\)，\(Y\) の共分散を \(S_{XY}\) とおくと
\(S_{XY}=\displaystyle\frac{1}{8}\left\{(6-6)(4-5)+(8-6)(3-5)+(6-6)(5-5)\\+(10-6)(2-5)+(4-6)(6-5)+(6-6)(7-5)\\+(2-6)(7-5)+(6-6)(6-5)\right\}=-\displaystyle\frac{13}{4}\)
よって相関係数 \(r\) は
\(r=\displaystyle\frac{S_{XY}}{S_{X}S_{Y}}=\displaystyle\frac{-\frac{13}{4}}{\sqrt{5}\sqrt{3}}=-\displaystyle\frac{13}{4\sqrt{15}}\)
ちなみに，\(r=\displaystyle\frac{13}{4\sqrt{15}}=-0.839\cdots\)
となります．
(３) \(2\) 次不等式
\(x^2-5ax+6a^2≦0\) ・・・①，\(x^2-2ax+a^2-1≦0\) ・・・②
①より
\((x-2a)(x-3a)≦0\)
\(a>0\) より \(2a<3a\) であるから
\(2a≦x≦3a\)
②より
\(x^2-2ax+(a-1)(a+1)≦0\)
\(\left\{x-(a-1)\right\}\left\{x-(a+1)\right\}≦0\)
\(a>0\) より \(a-1<a+1\) であるから
\(a-1≦x≦a+1\)
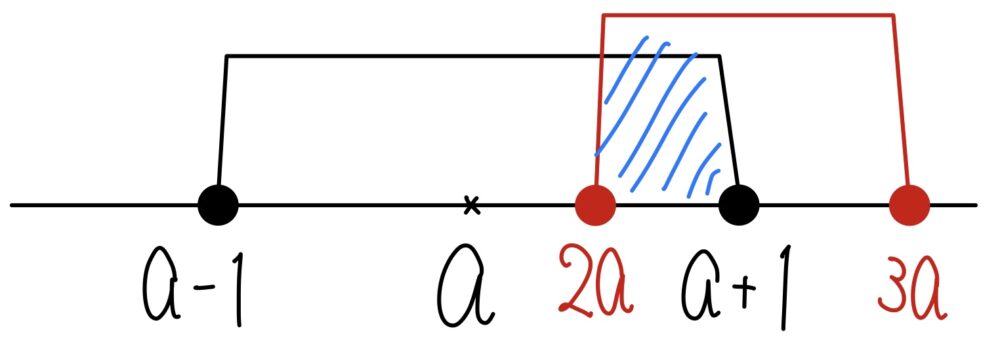\(a-1≦x≦a+1\) の真ん中の値が \(a\) である事に注目すると，
\(a>0\) より \(a<2a\) であるから，\(2a\) は必ず \(a-1\) よりも右側にあることがわかりますね！
①，②を同時にみたす実数 \(x\) が存在するとき
\(2a≦a+1\) \(\iff\) \(a≦1\)
\(a>0\) より，\(0<a≦1\) ・・・( b )
(４) 整数問題(合同式を利用した別解あ)
まず初めに，下 \(1\) 桁(一の位) に注目する．
\(2\) 乗しても下 \(1\) 桁がもとの数と一致する数は，
「 \(0\) ，\(1\) ，\(5\) ，\(6\) 」のいずれか．
よって \(1≦a≦9\) を満たす整数 \(a\) を用いて，
\(n=10a\)，\(10a+1\)，\(10a+5\)，\(10a+6\) のいずれかの形で表すことができる．
( ⅰ ) \(n=10a\) のとき
\(n^2=100a^2\) となり，\(n^2\) の下 \(2\) 桁の数は「 \(00\) 」となるので不適．
( ⅱ ) \(n=10a+1\) のとき
\(n^2=100a^2+20a+1\) より，
\(n^2\) の下 \(2\) 桁の数は，\(20a+1\) の下 \(2\) 桁の数に等しい．
ここで，\(a=1,2,\cdots,9\) としたとき，
\(n=10a+1\) と \(20a+1\) の下 \(2\) 桁の数が等しくなることはない．
よって不適である．
( ⅲ ) \(n=10a+5\) のとき
( ⅱ ) と同様に考えると，\(a=2\) のとき成り立つ
よって，\(n=25\) のとき成り立つ
(※\(25^2=625\) となり成立)
( ⅳ ) \(n=10a+6\) のとき
( ⅱ ) と同様に考えると，\(a=7\) のとき成り立つ
よって，\(n=76\) のとき成り立つ
(※\(76^2=5776\) となり成立)
したがって，条件を満たす \(n\) は \(2\) 個 ・・・( a )
コメント