フェルマーの小定理

はじめに

大学受験（整数問題）において、フェルマーの小定理を知っていると簡単に処理できる入試問題は定期的に出題されています。（もちろん知らなくても解けますが・・・）

整数問題を極めようと思えば、ぜひ一度は触れておきたいテーマの１つになりますので、整数問題を武器にしたい人はぜひ下記を読んでください！

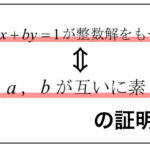
また、下記では合同式を利用します．合同式に不安がある人は、

合同式とは？合同式の基本性質を理解し、使えるようにする

合同式（基本編）基本的な問題で合同式を使う練習

を用いて練習をしてから読んでください．

【補題】証明のための準備

証明

\(ma\) と \(na\) \(( 1 ≦ m < n < p )\) を \(p\) で割った余りが等しいと仮定する．

つまり、

\(na-ma = (n-m)a\) は \(p\) の倍数・・・（※）

となるが、

\( 1 ≦ n-m < p\) かつ \(a , p\) は互いに素であるから、

\((n-m)a\) が \(p\) の倍数であることは矛盾．

したがって、

\(a , p\) が互いに素なとき、\(a , 2a , 3a , \cdots , (p-1)a\) を \(p\) で割った余りはすべて異なる

【参考】（※）について

フェルマーの小定理の証明

【証明】

上の補題より

\(a , p\) が互いに素なとき、\(a , 2a , 3a , \cdots , (p-1)a\) を \(p\) で割った余りはすべて異なるので、

法を \(p\) として

\(a \times 2a \times 3a \times \cdots \times (p-1)a ≡ 1 \times 2 \times 3 \cdots \times (p-1)\)

\((p-1)! \times a^{p-1} ≡ (p-1)!\)

\(p\) と \((p-1)!\) は互いに素であるから

\(a^{p-1} ≡ 1\)    \(( mod p )\)

【参考解説（具体例）】

\(a=3 , p=5\) として考える

\(3 , 2\times 3 , 3\times 3 ,  4\times 3\) を \(5\) で割った余りを考えると

法を \(5\) として

\(3 ≡ 3\) , \(2\times 3≡ 1\) , \(3\times 3≡ 4\) , \(4\times 3≡ 2\) より

\(3 \times (2\times 3) \times (3\times 3) \times (4\times 3) ≡ 3 \times 1 \times 4 \times 2\)

上の証明では、右辺のかけ算の順番を並び替えました！

よって、

\(4! \times 3^4 ≡ 4!\)

\(5\) と \(4!\) は互いに素であるから

\(3^4 ≡ 1\)    \(( mod 5 )\)

最後に

いかがだったでしょうか？

少し難しいテーマになりました。

初めましての場合、完璧に全てを理解するのは難しいかもしれません。

ただフェルマーの小定理を背景とした入試問題は難関大学では不定期に出題されていますので、証明はさておき、結論を知っているかどうかがまずは大切です。

整数問題の分野では、使える道具が多ければ多いほど、簡単に処理できることが多いので、ここでは１つの知識としてフェルマーの小定理を身につけてください！

他にも学校では扱わないが入試頻出テーマをたくさん扱っています。志望校合格にお役立てください。