媒介変数で表された点の軌跡｜学習院大学

\(x=\displaystyle\frac{2t}{t^2+1}\) ・・・①

\(y=\displaystyle\frac{2t^2}{t^2+1}\) ・・・②

とおくと，①，②より \(y=tx\) ・・・③

\(t>0\) より，①から \(x>0\) であるから

③より，\(t=\displaystyle\frac{y}{x}\) ・・・④

④を①に代入すると，

\(x=\displaystyle\frac{2\left(\displaystyle\frac{y}{x}\right)}{\left(\displaystyle\frac{y}{x}\right)^2+1}\)

\(\iff\) \(x^2+y^2-2y=0\)

\(\iff\) \(x^2+(y-1)^2=1\)

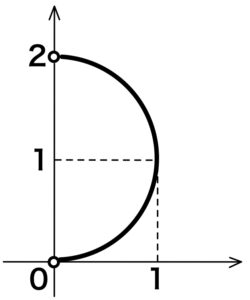
したがって求める軌跡の方程式は，

円 \(x^2+(y-1)^2=1\) の \(x>0\) の部分

これを図示すると，次図の太線部分 ( 点 \(( 0 , 0 ) , ( 0 , 2 )\) を除く)

参考：発展的な別解

\(t\) は正の実数値をとって変化するので

\(t=\tan\displaystyle\frac{\theta}{2}\) ( \(0<\theta<\pi\) ) とおけます．

これを使って \(x\) , \(y\) をそれぞれ \(\theta\) の式で表すと，

\(x=\sin \theta\) , \(y=1-\cos \theta\) と得られるので，

\(\sin^2 \theta+\cos^2 \theta=1\) を利用すれば

\(x^2+(y-1)^2=1\) の結果を導くことができます！

また，\(0<\theta<\pi\) のとき，\(x>0\) であることも確認できます！

このタイプの置換はとても有名ですね！

三角関数の差がつく問題の１つです！

「t=tan(x/2)のとき，sinx,cosx,tanxをtを用いて表せ｜三角関数」を参考に。