【問題】一橋大学 過去問
\(a , b\) を実数として、\(P=a^4-4a^2b+b^2+6b\) とおく．
(1) すべての実数 \(b\) に対して \(P≧0\) となるような \(a\) の値の範囲を求めよ．
(2) すべての実数 \(a\) に対して \(P≧0\) となるような \(b\) の値の範囲を求めよ．
考え方・思考の仕方・解答
ある範囲において \(f(x)≧0\)
☞ (ある範囲における \(f(x)\) の最小値) \(≧0\)
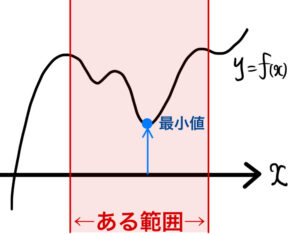
例えば図のような \(y=f(x)\) を考える．
「ある範囲において \(f(x)≧0\)」であるとは、
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」
と言う状態を表す．
「ある範囲で \(y=f(x)\) が \(x\) 軸より上側にある 」ことを言うためには、
「\(y=f(x)\) の最小値が \(x\) 軸より上側にある」ことが言えればよい．
すべての○○に対して・・・
☞ ○○の関数と考える．
(1)考え方
すべての実数 \(b\) に対して・・・より、
\(b\) の関数と考え(\(a\) は定数扱い)、
\(b\) について降べきの順に並べると、
\(P=b^2-2(a^2-3)b+a^4\)
つまり \(b\) の 2 次関数として扱う．
Pointと合わせて考えると、
\(f(b)=b^2-2(2a^2-3)b+a^4\) とおけば、
「すべての実数 \(b\) で、 2 次関数 \(f(b)≧0\) 」と言う問題．
よって、
すべての実数 \(b\) における
2 次関数 \(f(b) \) の最小値を考え、それが 0 以上であることを言えばよい．
(1)解答
\(f(b)=b^2-2(2a^2-3)b+a^4\) とおく．
平方完成を行うと、
\(f(b)=(b-2a^2+3)^2-3a^4+12a^2-9\)
\(b=2a^2-3\) のとき
\(f(b)\) の最小値は \(-3a^4+12a^2-9\)
したがって題意を満たすとき、
\(-3a^4+12a^2-9≧0\)
\(a^4-4a^2+3≦0\)
\((a^2-1)(a^2-3)≦0\)
\(1≦a^2≦3\)
したがって、\(-\sqrt{3}≦a≦-1 , 1≦a≦\sqrt{3}\)
(2)考え方
(1)同様に考え、\(a\) について降べきの順に並べると、
\(P=a^4-4ba^2+b^2+6b\)
つまり \(a\) の 4 次関数として扱う．
えっ！？ 4 次関数の最小値を考えるの？？
・・・と言うことは、微分して増減表？？
もちろんそれでも悪くはないけど、できれば 4 次関数は避けたいよね！
だから工夫しましょう！
\(a^2\) を何か文字で置けば 2 次関数にできる！！
その通り！
ただし、１点注意しなければいけないことがあるね！
範囲の確認だね！
何か置き換えたときは必ず範囲を確認するのは受験数学でのお約束だったね！
例えば、\(t=a^2\) と置き換えると、\(t≧0\) になるね！
だから今回の問題は、
\(t≧0\) において、\(t\) の 2 次関数の最小値が 0 以上になればよいってこと！
(2)解答
\(a\) について降べきの順に並べると、
\(P=a^4-4ba^2+b^2+6b\)
ここで、\(t=a^2\) とおく．
このとき \(t≧0\) となる．
よって
\(P=t^2-4bt+b^2+6b=g(t)\) とおく．
本問では、
\(t≧0\) において、\(g(t)≧0\) を考えればよい．
つまり、
\(t≧0\) における、\(g(t)\) の最小値が 0 となる範囲を考えればよい．
\(g(t)=(t-2b)^2-3b^2+6b\) より
(ⅰ) \(2b<0\)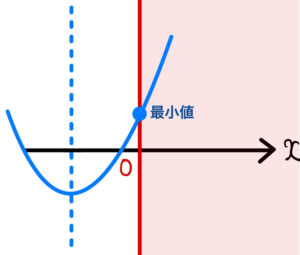 
つまり \(b<0\) のとき
\(t≧0\) における、\(g(t)\) の最小値は \(g(0)=b^2+6b\)
したがって、\(b^2+6b≧0\)
\(b(b+6)≧0\)
\(b≦-6 , 0≦b\)
\(b<0\) のときであるから、
\(b≦-6 \)
(ⅱ) \(0≦2b\)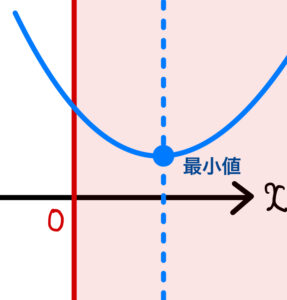
つまり \(0≦b\) のとき
\(t≧0\) における、\(g(t)\) の最小値は \(g(2b)=-3b^2+6b\)
したがって、\(-3b^2+6b≧0\)
\(b^2-2b≦0\)
\(b(b-2)≦0\)
\(0≦b≦2\) (これは \(0≦b\) を満たす)
以上より、\(b≦-6 \)、\(0≦b≦2\)
最後に
今回のテーマのPointは、関数の問題において最頻出です。
本問では結果的に 2 次関数として扱いましたが、3 次関数など(数学Ⅲでは何でもあり)形を変えて出題されます．また不等式の証明としても利用できるので、しっかりと考え方をおさえましょう！
コメント