【2021広島大学】
(１) \(A=\sin x\) とおく．\(\sin 5x\) を \(A\) の整式で表せ．
(２) \(\sin^2\displaystyle\frac{\pi}{5}\) の値を求めよ．
(３) 曲線 \(y=\cos 3x\) ( \(x≧0\) ) と曲線 \(y=\cos7x\) ( \(x≧0\) ) の共有点の \(x\) 座標を小さい方から順に \(x_{1}\) , \(x_{2}\) , \(x_{3}\) , \(\cdots\) とする．このとき，関数 \(y=\cos 3x\) ( \(x_{5}≦x≦x_{6}\) ) の値域を求めよ．
(１) \(\sin 5x\) を \(\sin x\) で表せ
加法定理や 2 倍角，3 倍角の公式など，三角関数の公式をたくさん利用します。
公式がしっかりと覚えられていない人は，「【三角関数】公式まとめ&差がつく入試問題演習」で今一度公式を確認しましょう！
(１)解答・解説
\(\sin 5x=\sin (3x+2x)\)
\(=\sin 3x\cos 2x+\cos 3x\sin 2x\)
\(=(3\sin x-4\sin^3x)(1-2\sin^2x)+(4\cos^3-3\cos x)\cdot 2\sin x\cos x\)
\(=8\sin^5 x-10\sin^3 x+3\sin x+2\sin x\cos^2 x(4\cos^2x-3)\)
\(A=\sin x\) とおくと，\(\cos^2x=1-\sin^2x=1-A^2\) より
\(\sin 5x=8A^5-10A^3+3A+2A(1-A^2)\left\{4(1-A^2)-3\right\}\)
\(=8A^5-10A^3+3A+2A(1-A^2)(1-4A^2)\)
\(=16A^5-20A^3+5A\)
(２) \(\sin^2\displaystyle\frac{\pi}{5}\) の値
(２)解答・解説
\(x=\displaystyle\frac{\pi}{5}\) のとき，\(\sin 5x=0\) なので，
\(A=\sin \displaystyle\frac{\pi}{5}\) とすると，(１) より
\(16A^5-20A^3+5A=0\)
\(A(16A^4-20A^2+5)=0\)
\(A=\sin \displaystyle\frac{\pi}{5}\not=0\) より
\(16A^4-20A^2+5=0\)
\(16(A^2)^2-20A^2+5=0\)
\(A^2=\displaystyle\frac{5\pm\sqrt{5}}{8}\)
\(A=\sin \displaystyle\frac{\pi}{5}<\sin \displaystyle\frac{\pi}{4}=\displaystyle\frac{1}{\sqrt{2}}\) より
\(A^2=\sin^2 \displaystyle\frac{\pi}{5}<\displaystyle\frac{1}{2}\) であるから
\(A^2=\displaystyle\frac{5-\sqrt{5}}{8}\)
(３) \(\cos A=\cos B\) について
考え方①単位円で考える
\(\cos A=\cos B\)
\(\iff\) \(A=\pm B+2n\pi\) ( \(n\) は整数 )
考え方②和積の公式の利用
和積の公式
\(\cos A-\cos B=-2\sin\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\)
考え方①，②についての詳細は，
「【2012京都大学】cos aθ=cos bθ，0<θ≦πとなるθがちょうど1つある正の実数(a,b)の範囲」を参考に！
(３)解答・解説
\(\cos 7x=\cos 3x\)
\(\iff\) \(7x=\pm3x+2n\pi\) ( \(n\) は整数 )
\(\iff\) \(x=\displaystyle\frac{n\pi}{2}\) または \(x=\displaystyle\frac{n\pi}{5}\)
\(x≧0\) を満たすものを小さい順に並べると，
\(x = 0 , \displaystyle\frac{\pi}{5} , \displaystyle\frac{2\pi}{5} , \displaystyle\frac{\pi}{2} , \displaystyle\frac{3\pi}{5} , \displaystyle\frac{4\pi}{5} , \cdots\)
よって，\(x_{5}=\displaystyle\frac{3\pi}{5}\) , \(x_{6}=\displaystyle\frac{4\pi}{5}\)
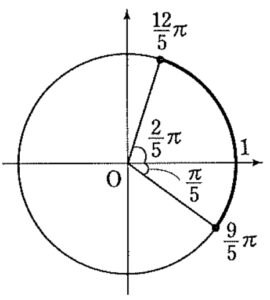\(y=\cos 3x\) ( \(x_{5}≦x≦x_{6}\) ) において
\(\displaystyle\frac{9\pi}{5}≦3x≦\displaystyle\frac{12\pi}{5}\) であるから
求める値域は，
\(\cos \displaystyle\frac{12\pi}{5}≦y≦1\) ・・・①
ここで，\(\cos \displaystyle\frac{12\pi}{5}=\cos \displaystyle\frac{2\pi}{5}=1-2\sin^2\displaystyle\frac{\pi}{5}=1-2A^2\)
(２)より \(A^2=\displaystyle\frac{5-\sqrt{5}}{8}\) であるから
\(\cos \displaystyle\frac{12\pi}{5}=1-2\cdot\displaystyle\frac{5-\sqrt{5}}{8}=\displaystyle\frac{\sqrt{5}-1}{4}\)
したがって①より，
\(\displaystyle\frac{\sqrt{5}-1}{4}≦y≦1\)
コメント