【問題】\(0≦x<2\pi\) のとき，次の関数の最大値と最小値を求めよ．
(１) \(y=5\cos^2x+6\sin x\cos x-3\sin^2x\)
(２) \(y=\sqrt{2}(\sin x+\cos x)-\sin x\cos x-1\)
\(\sin x\cos x\) を含む関数の最大・最小の解法２パターン
方針①半角の公式 ⇒ 三角関数の合成
与式の中に，\(\sin x\cos x\) 以外に『 \(\sin^2x\) , \(\cos^2x \) 』を含むとき
半角の公式を利用し，三角関数の合成へ！
半角の公式
三角関数の合成
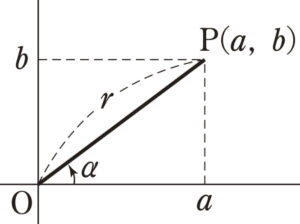\(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin (\theta+\alpha)\)
ただし，\(\sin \alpha=\displaystyle\frac{b}{\sqrt{a^2+b^2}}\)
\(\cos \alpha=\displaystyle\frac{a}{\sqrt{a^2+b^2}}\)
方針②置き換え，式変形，範囲の確認
与式に \(\sin x\cos x\) 以外に『 \(\sin x+\cos x\) 』の形を含むとき
\(t=\sin x+\cos x\) と置き換え&式変形&範囲の確認
置き換えをしたら必ず \(t\) の範囲の確認をする癖を！
解答
(１)解答
\(0≦x<2\pi\) のとき，次の関数の最大値と最小値を求めよ．
(１) \(y=5\cos^2x+6\sin x\cos x-3\sin^2x\)
\(\sin^2x=\displaystyle\frac{1-\cos 2x}{2}\) , \(\cos^2x=\displaystyle\frac{1+\cos 2x}{2}\)
また，\(\sin x\cos x=\displaystyle\frac{1}{2}\sin 2x\) より
\(y=5\cdot\displaystyle\frac{1+\cos 2x}{2}+6\cdot\displaystyle\frac{1}{2}\sin 2x-3\cdot\displaystyle\frac{1-\cos 2x}{2}\)
\(=3\sin 2x+4\cos 2x+1\)
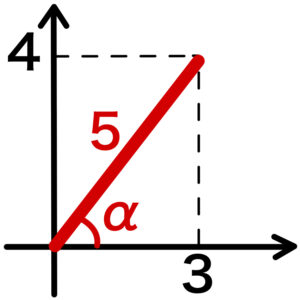
\(=5\sin(2x+\alpha)+1\)
ただし，\(\sin \alpha=\displaystyle\frac{4}{5}\) , \(\cos \alpha=\displaystyle\frac{3}{5}\)
\(0≦x<2\pi\) のとき
\(-1≦\sin (2x+\alpha)≦1\) より
\(-4≦5\sin (2x+\alpha)+1≦6\)
\(-4≦y≦6\)
したがって，最大値： \(6\) , 最小値： \(-4\)
(２)解答
【問題】\(0≦x<2\pi\) のとき，次の関数の最大値と最小値を求めよ．
(２) \(y=\sqrt{2}(\sin x+\cos x)-\sin x\cos x-1\)
\(t=\sin x+\cos x\) とおく．
\(t^2=\sin^2 x+2\sin x\cos x+\cos^2 x\) より
\(\sin x\cos x=\displaystyle\frac{t^2-1}{2}\) であるから
\(y=\sqrt{2}t-\displaystyle\frac{t^2-1}{2}-1\)
よって，
\(y=-\displaystyle\frac{1}{2}t^2+\sqrt{2}t-\displaystyle\frac{1}{2}\)
\(y=-\displaystyle\frac{1}{2}(t-\sqrt{2})^2+\displaystyle\frac{1}{2}\) ・・・①
また，\(t=\sin x+\cos x\) より
\(t=\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)\)
\(0≦x<2\pi\) のとき
\(-1≦\sin \left(x+\displaystyle\frac{\pi}{4}\right)≦1\) より
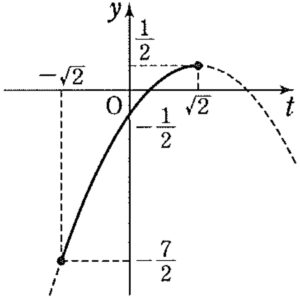\(-\sqrt{2}≦t≦\sqrt{2}\) ・・・②
①，②より
\(t=\sqrt{2}\) で最大値：\(\displaystyle\frac{1}{2}\)
\(t=-\sqrt{2}\) で最大値：\(-\displaystyle\frac{7}{2}\)
\(t=\sqrt{2}\) のとき
\(\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)=\sqrt{2}\)
\(\sin \left(x+\displaystyle\frac{\pi}{4}\right)=1\)
\(\displaystyle\frac{\pi}{4}≦x+\displaystyle\frac{\pi}{4}<\displaystyle\frac{9\pi}{4}\) より
\(x+\displaystyle\frac{\pi}{4}=\displaystyle\frac{\pi}{2}\)
よって，\(x=\displaystyle\frac{\pi}{4}\) のとき最大値：\(\displaystyle\frac{1}{2}\)
\(t=-\sqrt{2}\) のとき
\(\sqrt{2}\sin \left(x+\displaystyle\frac{\pi}{4}\right)=-\sqrt{2}\)
\(\sin \left(x+\displaystyle\frac{\pi}{4}\right)=-1\)
\(\displaystyle\frac{\pi}{4}≦x+\displaystyle\frac{\pi}{4}<\displaystyle\frac{9\pi}{4}\) より
\(x+\displaystyle\frac{\pi}{4}=\displaystyle\frac{3\pi}{2}\)
よって，\(x=\displaystyle\frac{5\pi}{4}\) のとき最大値：\(-\displaystyle\frac{7}{2}\)
コメント