【2012京都大学】
正四面体 \(OABC\) において，点 \(P\) , \(Q\) , \(R\) をそれぞれ辺 \(OA\) , \(OB\) , \(OC\) 上にとる．
ただし \(P\) , \(Q\) , \(R\) は四面体 \(OABC\) の頂点とは異なるとする．\(\triangle PQR\) が正三角形ならば，\(3\) 辺 \(PQ\) , \(QR\) , \(RP\) はそれぞれ \(3\) 辺 \(AB\) , \(BC\) , \(CA\) に平行であることを証明せよ．
考え方・方針
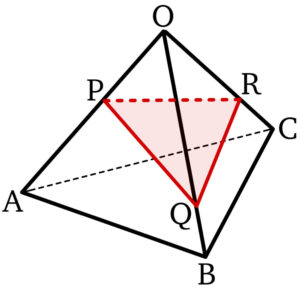\(PQ // AB\) , \(QR // BC\) , \(RP // CA\) であることを示すためには，
\(OP:OA=OQ:OB=OR:OC\) であることが示せればよい．
ここで，正四面体 \(OABC\) であり，「比」が分かれば良いので，
\(OA=OB=OC=1\) として一般性を失わない．
したがって，実数 \(s\) , \(t\) , \(u\) は \(0<s<1\) , \(0<t<1\) , \(0<u<1\) として
\(\overrightarrow{OP}=s\overrightarrow{OA}\) , \(\overrightarrow{OQ}=t\overrightarrow{OB}\) , \(\overrightarrow{OR}=u\overrightarrow{OC}\) のとき，
\(s=t=u\) を示すことが出来ればよい．
\(OA=OB=OC=1\) とおくことで，煩雑な計算を簡略化することができる！
解答
正四面体 \(OABC\) の \(1\) 辺の長さを \(1\) として一般性を失わない．
\(\overrightarrow{OA}=\overrightarrow{a}\) , \(\overrightarrow{OB}=\overrightarrow{b}\) , \(\overrightarrow{OC}=\overrightarrow{c}\) とおく．
このとき，
\(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=1\) かつ
\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}=\displaystyle\frac{1}{2}\) ・・・①
ここで，\(\overrightarrow{OP}=s\overrightarrow{a}\) , \(\overrightarrow{OQ}=t\overrightarrow{b}\) , \(\overrightarrow{OR}=u\overrightarrow{c}\) とおく．
ただし \(s\) , \(t\) , \(u\) は \(0<s<1\) , \(0<t<1\) , \(0<u<1\) をみたす実数．
仮定より \(\triangle PQR\) が正三角形であるから，
\(\left|\overrightarrow{PQ}\right|=\left|\overrightarrow{PR}\right|\)
\(\left|\overrightarrow{OQ}-\overrightarrow{OP}\right|=\left|\overrightarrow{OR}-\overrightarrow{OP}\right|\)
\(2\) 乗して式をまとめると
\(\left|\overrightarrow{OQ}\right|^2-\left|\overrightarrow{OR}\right|^2-2\left(\overrightarrow{OP}\cdot\overrightarrow{OQ}-\overrightarrow{OP}\cdot\overrightarrow{OR}\right)\)
よって，\(t^2\left|\overrightarrow{b}\right|^2-u^2\left|\overrightarrow{c}\right|^2-2\left(st\overrightarrow{a}\cdot\overrightarrow{b}-su\overrightarrow{a}\cdot\overrightarrow{c}\right)\)
①より，\(t^2-u^2-st+su=0\)
\((t-u)(t+u)-s(t-u)=0\)
\((t-u)(t+u-s)=0\)
よって，\(t=u\) または \(s=t+u\) ・・・②
次に， \(\triangle PQR\) が正三角形であるから，
\(\overrightarrow{PQ}\cdot\overrightarrow{PR}=\left|\overrightarrow{PQ}\right|\left|\overrightarrow{PR}\right|cos 60°\)
\(\left(\overrightarrow{OQ}-\overrightarrow{OP}\right)\cdot\left(\overrightarrow{OR}-\overrightarrow{OP}\right)=\displaystyle\frac{1}{2}\left|\overrightarrow{OQ}-\overrightarrow{OP}\right|^2\)
\(\left(t\overrightarrow{b}-s\overrightarrow{a}\right)\cdot\left(u\overrightarrow{c}-s\overrightarrow{a}\right)=\displaystyle\frac{1}{2}\left|t\overrightarrow{b}-s\overrightarrow{a}\right|^2\)
これを展開し①を代入して式をまとめると
\(s^2-t^2-su+tu=0\)
\((s-t)(s+t)-u(s-t)=0\)
\((s-t)(s+t-u)=0\) ・・・③
②より，
( ⅰ ) \(t=u\) のとき
③ \(\iff\) \((s-u)s=0\)
\(0<s<1\) であるから，\(s=u\)
したがって，\(s=t=u\)
( ⅱ ) \(s=t+u\) のとき
③ \(\iff\) \(2tu=0\)
\(t=0\) または \(u=0\) となるが，これは \(0<t<1\) , \(0<u<1\) に不適
以上より，\(s=t=u\) であるから
\(OP:OA=OQ:OB=OR:OC\)
つまり，\(PQ // AB\) , \(QR // BC\) , \(RP // CA\) が成り立つ．
コメント