【2003京都大学】
四面体 \(OABC\) は次の \(2\) つの条件
( ⅰ ) \(\overrightarrow{OA}\perp\overrightarrow{BC}\) , \(\overrightarrow{OB}\perp\overrightarrow{AC}\) , \(\overrightarrow{OC}\perp\overrightarrow{AB}\)
( ⅱ ) \(4\) つの面の面積がすべて等しい
をみたしている.このとき,この四面体は正四面体であることを示せ.
考え方・方針の立て方
条件( ⅰ )ベクトルで垂直⇒内積が \(0\)
まず条件( ⅰ )において,ベクトルで垂直に関する条件があれば,内積が \(0\) になることを疑ってほしい!
条件( ⅱ )ベクトルにおける面積公式
最重要公式の1つです!この公式は分野問わずに使いこなせるように!
解答
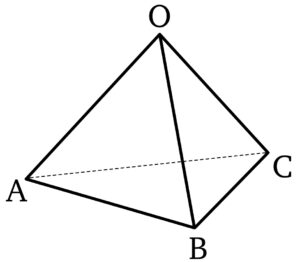 \(\overrightarrow{OA}=\overrightarrow{a}\) ,\(\overrightarrow{OB}=\overrightarrow{b}\) ,\(\overrightarrow{OC}=\overrightarrow{c}\) とおく.
\(\overrightarrow{OA}=\overrightarrow{a}\) ,\(\overrightarrow{OB}=\overrightarrow{b}\) ,\(\overrightarrow{OC}=\overrightarrow{c}\) とおく.
条件( ⅰ )より
\(\begin{cases}\overrightarrow{OA}\cdot\overrightarrow{BC}=\overrightarrow{a}\cdot(\overrightarrow{c}-\overrightarrow{b})=\overrightarrow{c}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}=0\\\overrightarrow{OB}\cdot\overrightarrow{AC}=\overrightarrow{b}\cdot(\overrightarrow{c}-\overrightarrow{a})=\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{a}\cdot\overrightarrow{b}=0\\\overrightarrow{OC}\cdot\overrightarrow{AB}=\overrightarrow{c}\cdot(\overrightarrow{b}-\overrightarrow{a})=\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{c}\cdot\overrightarrow{a}=0\end{cases}\)
よって,\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}\) ・・・①
次に,
\(\triangle OAB=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{a}\right|^2\left|\overrightarrow{b}\right|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2}\)
\(\triangle OBC=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{b}\right|^2\left|\overrightarrow{c}\right|^2-\left(\overrightarrow{b}\cdot\overrightarrow{c}\right)^2}\)
\(\triangle OCA=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{c}\right|^2\left|\overrightarrow{a}\right|^2-\left(\overrightarrow{c}\cdot\overrightarrow{a}\right)^2}\)
より,条件( ⅱ )から
\(\sqrt{\left|\overrightarrow{a}\right|^2\left|\overrightarrow{b}\right|^2-\left(\overrightarrow{a}\cdot\overrightarrow{b}\right)^2}=\sqrt{\left|\overrightarrow{b}\right|^2\left|\overrightarrow{c}\right|^2-\left(\overrightarrow{b}\cdot\overrightarrow{c}\right)^2}=\sqrt{\left|\overrightarrow{c}\right|^2\left|\overrightarrow{a}\right|^2-\left(\overrightarrow{c}\cdot\overrightarrow{a}\right)^2}\)
①より,
\(\left|\overrightarrow{a}\right|^2\left|\overrightarrow{b}\right|^2=\left|\overrightarrow{b}\right|^2\left|\overrightarrow{c}\right|^2=\left|\overrightarrow{c}\right|^2\left|\overrightarrow{a}\right|^2\)
よって,\(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|\) ・・・②
また①より,
\(\left|\overrightarrow{a}\right|\left|\overrightarrow{b}\right|\cos \angle AOB=\left|\overrightarrow{b}\right|\left|\overrightarrow{c}\right|\cos \angle BOC=\left|\overrightarrow{c}\right|\left|\overrightarrow{a}\right|\cos \angle COA\)
であり②から
\(\cos \angle AOB=\cos \angle BOC=\cos \angle COA\)
よって \(\angle AOB=\angle BOC=\angle COA\) ・・・③
②,③より \(3\) つの側面 \(\triangle OAB\) , \(\triangle OBC\) ,\(\triangle OCA\) は互いに合同な二等辺三角形となる.
ゆえに,底面 \(\triangle ABC\) は正三角形となる.
次に,\(\triangle OAB\) と \(\triangle ABC\) について考えると,これらの三角形は底辺 \(AB\) を共有する二等辺三角形であり,条件( ⅱ )から面積が等しい.したがって高さがそれぞれ等しいため,この \(2\) つの三角形は合同となる.つまり,\(\triangle OAB\) は正三角形となる.
したがって,四面体 \(OABC\) は正四面体となる.





コメント