【2023兵庫医科大学】|x|+|y|の最大・最小(線形計画法)

【2023兵庫医科大学】

実数 \(x\)，\(y\) が \(x^2-2x+y^2-3=0\) を満たすとき，

( a )　\(|x|+|y|\) の最小値とそのときの \(x\) および \(y\) の値を求めよ．

( b )　\(|x|+|y|\) の最大値とそのときの \(x\) および \(y\) の値を求めよ．

解答・解説

\(x^2-2x+y^2-3=0\) \(\iff\) \((x-1)^2+y^2=4\) より

実数 \(x\)，\(y\) は中心 \((1,0)\) ，半径 \(2\) の円上を動く．

\(|x|+|y|=k\) ( \(k>0\) ) ・・・① とおくと，

これは \(4\) 点 \((k,0)\)，\((0,k)\)，\((-k,0)\)，\((0,-k)\) を頂点とする正方形を表す．

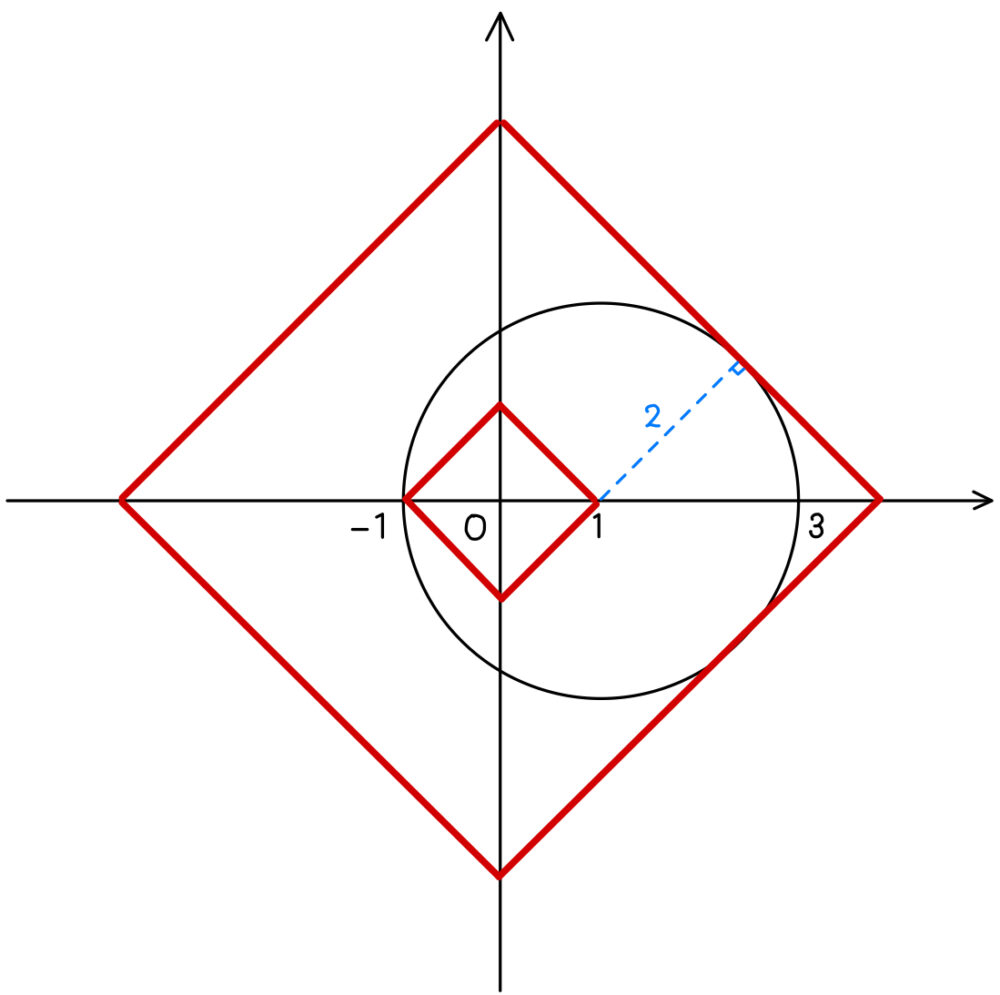
( a )　\(|x|+|y|\) が最小となるのは上図より

①が \((-1,0)\) を通るとき，最小値：\(1\)

( b )　\(|x|+|y|\) が最大となるのは上図より

①が \((x-1)^2+y^2=4\) と第 \(1\) 象限または第 \(4\) 象限で接するときである．

第 \(1\)，\(4\) 象限について考えるので，\(x>0\)

このとき，①は \(x\pm y=k\)

円の中心 \((1,0)\) から直線 \(x\pm y-k=0\) までの距離が \(2\) (円の半径)となればよいので，

\(\displaystyle\frac{|1-k|}{\sqrt{2}}=2\) \(\iff\) \(k=1\pm 2\sqrt{2}\)

\(k>0\) より \(k=1+2\sqrt{2}\)

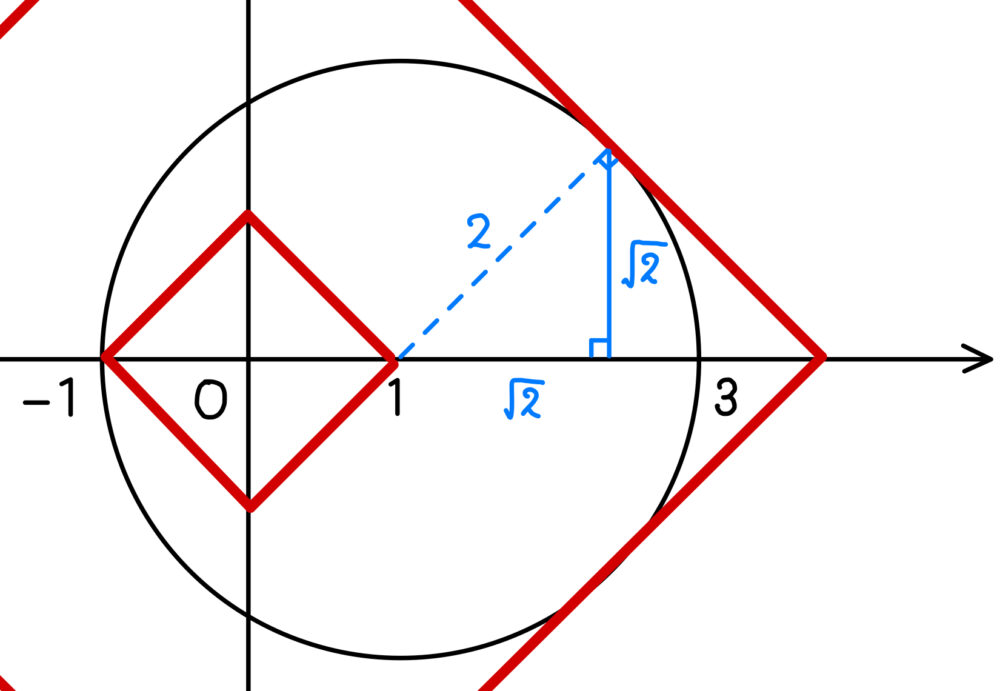また右図から，\(1：1：\sqrt{2}\) の直角二等辺三角形に注目すると，

接点は \((1+\sqrt{2},\sqrt{2})\) または \((1+\sqrt{2},-\sqrt{2})\)

したがって，

\((1+\sqrt{2},\pm\sqrt{2})\) のとき最大値： \(1+2\sqrt{2}\)