【2013京都大学・第４問】
\(-\displaystyle\frac{\pi}{2}≦x≦\displaystyle\frac{\pi}{2}\) における \(\cos x+\displaystyle\frac{\sqrt{3}}{4}x^2\) の最大値を求めよ．
ただし，\(\pi>3.1\) , \(\sqrt{3}>1.7\) が成り立つことは証明なしに用いてよい．
考え方
①偶関数・奇関数の利用
\(f(x)=\cos x+\displaystyle\frac{\sqrt{3}}{4}x^2\) とおくと，
\(f(-x)=\cos (-x)+\displaystyle\frac{\sqrt{3}}{4}(-x)^2=f(x)\) であるから，
\(y=f(x)\) は偶関数であるとわかる．
つまり，\(y\) 軸に関して対称なグラフとなるので，
\(0≦x≦\displaystyle\frac{\pi}{2}\) におけるグラフのみ考えれば，求める最大値はわかる．
最大・最小値の問題を見ると，とりあえず微分したくなりますが，まず初めに「偶関数・奇関数」について疑う習慣を！
これに気がつけるかどうかで，後々の計算量が半分に！！
偶関数とは
\(y\) 軸に関して対称なグラフ：\(f(x) = f(-x)\)
例：\(y=3\) (定数関数)、\(y=x^2\)、\(y=\cos x\) など
奇関数とは
原点に関して対称なグラフ：\(f(-x) = -f(x)\)
例：\(y=x\)、\(y=x^3\)、\(y=\sin x\)、\(y=\tan x\) など
②2次導関数の利用
\(f(x)=\cos x+\displaystyle\frac{\sqrt{3}}{4}x^2\) より
\(f^{\prime}(x)=-\sin x+\displaystyle\frac{\sqrt{3}}{2}x\)
\(f^{\prime}(x)=-\sin x+\displaystyle\frac{\sqrt{3}}{2}x=0\) となる \(x\) の値がわからない・・・(T . T)
そのような時は，\(y=f^{\prime}(x)\) と \(y=0\) ( \(x\) 軸 ) との交点として考えましょう！つまり，\(y=f^{\prime}(x)\) のグラフをかくために，もう一度微分(2次導関数)を求めましょう！
ややこしくなる方は，一度 \(g(x)=f^{\prime}(x)\) とでもおいて，\(y=g(x)\) のグラフをかくことに集中してみてください！
解答・解説
\(f(x)=\cos x+\displaystyle\frac{\sqrt{3}}{4}x^2\) とおくと，
\(f(-x)=\cos (-x)+\displaystyle\frac{\sqrt{3}}{4}(-x)^2=f(x)\) であるから，
\(y=f(x)\) は偶関数となる．
よって，\(0≦x≦\displaystyle\frac{\pi}{2}\) のときを考えればよい．
\(f^{\prime}(x)=-\sin x+\displaystyle\frac{\sqrt{3}}{2}x\)
ここで
\(g(x)=f^{\prime}(x)=-\sin x+\displaystyle\frac{\sqrt{3}}{2}x\) とおくと，
\(g^{\prime}(x)=-\cos x+\displaystyle\frac{\sqrt{3}}{2}\) より
\(0≦x≦\displaystyle\frac{\pi}{2}\) において \(g^{\prime}(x)=0\) となるのは，
\(x=\displaystyle\frac{\pi}{6}\) であるから
| \(x\) | \(0\) | ・・・ | \(\displaystyle\frac{\pi}{6}\) | ・・・ | \(\displaystyle\frac{\pi}{2}\) |
| \(g^{\prime}(x)\) | ー | \(0\) | ＋ | ||
| \(g(x)\) | \(0\) | ↘️ | ↗️ |
\(g(0)=0\)
\(g\left(\displaystyle\frac{\pi}{2}\right)=-1+\displaystyle\frac{\sqrt{3}}{4}\pi>-1+\displaystyle\frac{1.7\times 3.1}{4}=\displaystyle\frac{1.27}{4}>0\)
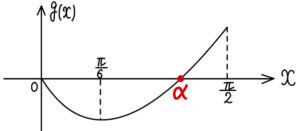であるから，\(y=g(x)\) のグラフの概形は次のようになる．
したがって，\(y=g(x)\) と \(y=0\) はただ \(1\) つの交点をもち，その値を \(x=\alpha\) ( \(\displaystyle\frac{\pi}{6}≦\alpha≦\displaystyle\frac{\pi}{2}\) ) とおくと，
\(0≦x≦\displaystyle\frac{\pi}{2}\) における \(g(x)=0\) の解は \(x=\alpha\) のみ
つまり，\(0≦x≦\displaystyle\frac{\pi}{2}\) における \(f^{\prime}(x)=0\) の解は \(x=\alpha\) のみ
よって，
| \(x\) | \(0\) | ・・・ | \(\alpha\) | ・・・ | \(\displaystyle\frac{\pi}{2}\) |
| \(f^{\prime}(x)\) | ー | \(0\) | ＋ | ||
| \(f(x)\) | \(1\) | ↘️ | ↗️ |
\(f(0)=1\) ,
\(f\left(\displaystyle\frac{\pi}{2}\right)=\displaystyle\frac{\sqrt{3}}{16}\pi^2>\displaystyle\frac{1.7\times 3.1^2}{16}=\displaystyle\frac{16.337}{16}>f(0)\)
となるので，
\(x=\pm\displaystyle\frac{\pi}{2}\) のとき，求める最大値は \(\displaystyle\frac{\sqrt{3}}{16}\pi^2\)
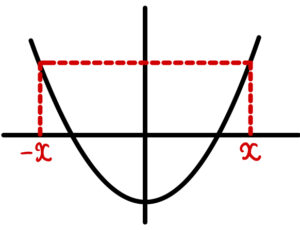
本問では偶関数として考えてきました。
最後に，左右対称の値も答えとなるため，
\(x=-\displaystyle\frac{\pi}{2}\) のときも最大値となります！
忘れないように注意しましょう！
コメント