【2016 京都大学】
素数 \(p , q\) を用いて \(p^q+q^p\)
と表される素数をすべて求めよ.
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
この3つのPointは絶対に頭の中に叩き込んでください!
はじめに
☆素数「2」は特別扱い
素数の中で唯一の偶数である「2」は、素数問題において特別扱いされることが非常に多い。
(※2番目の素数である「3」も特別扱いされることが多い)
その為、何も方針が浮かばないのであれば、とりあえず「2」や「3」あたりを確認してみると良い。
☆平方数・指数はmod 3,mod 4 が有効
難関大学ではよく出題されるPointの1つ!
まずは下の表を見てください。
平方数において
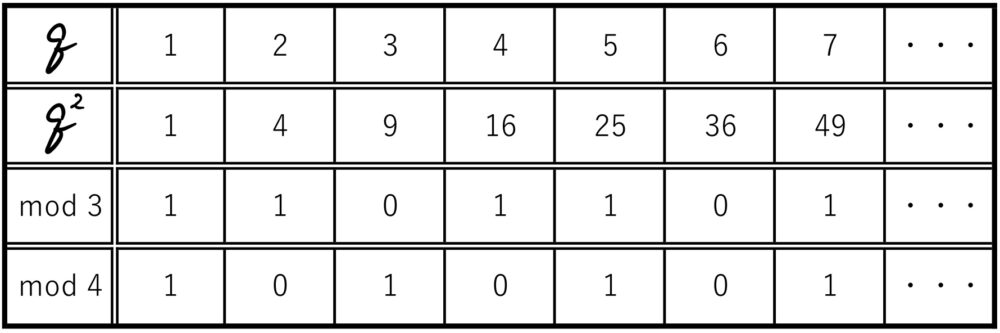
何かの2乗(平方数)において、
mod 3→「1,1,0」の繰り返し
mod 4→「1,0」の繰り返し
という規則が存在!
指数において
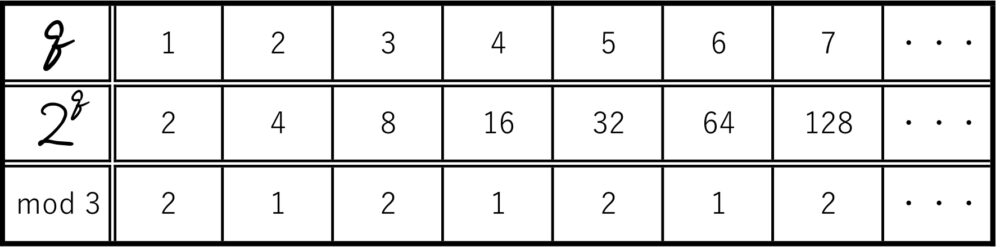
指数においてもmod 3,mod 4を考えることで規則性を見つけることが出来る!
【考え方・思考の仕方】
《Step1》
整数問題のPoint①の積の形には・・・無理だろう。
※できないと言うことを確認することが大切!
《Step2》整数問題のPoint②の範囲の絞り込みについて
\(p≧2 , q≧2\) より、
\(p^q+q^p≧2^2+2^2=8\)
つまり、
\(p^q+q^p\)は8以上の素数であるから、「奇数」であることが分かる
→\((p^q , q^p)=\)(偶数,奇数) または (奇数,偶数)
→\(p^q , q^p\) の一方が偶数、他方は奇数
→\(p , q\) の一方が偶数、他方は奇数
→\(p=2\) または \(q=2\)
→\(p=2\) のときをとりあえず考えよう!
《ここまでのまとめ》問題の言い換え
【問題】
素数 \(p , q\) を用いて \(p^q+q^p\)
と表される素数をすべて求めよ.
↓ 問題の言い換え ↓
・\(p=2\) かつ \(q\) は奇数の素数のとき、
\(2^q+q^2\) が素数となる \(q\) を求めたい.
《Step3》
整数問題のPoint③の倍数や余りに注目しつつ、とりあえず実験してみよう!
【具体的に実験した結果】

実験の結果から、とりあえず \(p=2 , q=3\) が答えであることは確定!
他に解はないことをしっかりと記述しよう!
《Step4》
\(q\) が5以上の素数のとき、
\(2^q+q^2\) が3の倍数になることを証明すればよい
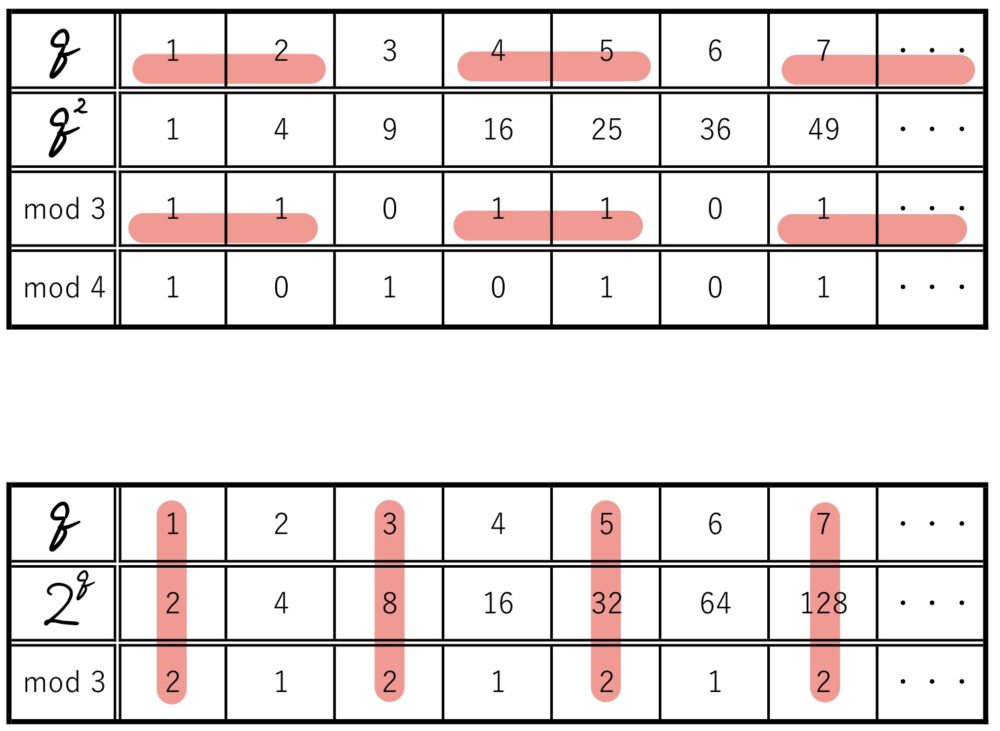
\(q\) が3の倍数でないのとき、
法を3とすると
\(q^2≡1\) ・・・①
\(q\) が奇数のとき、
法を3とすると
\(2^q≡2\) ・・・①
\(q\) が5以上の素数のとき、
\(2^q+q^2≡2+1≡0\)
となり\(2^q+q^2\) が3の倍数になる!!
【解答】
(ⅰ) \(p≦q\) のとき
\(2≦p≦q\) より、\(p^q+q^p≧2^2+2^2=8\)
つまり、
\(p^q+q^p\)は8以上の素数 ・・・① となる.
8以上の素数ならば奇数であるから
\(p^q , q^p\) の一方が偶数、他方は奇数
つまり\(p , q\) の一方が偶数、他方は奇数
よって\(p=2\)
(ア) \(q=3\) のとき
\(p^q+q^p=17\) となり、題意を満たす.
よって\((p , q)=(2 , 3)\)
(イ) \(q≧5\) の素数のとき
法を3として
\(2^q≡2\) ・・・②
(②の証明)
\(q≧5\) の素数より、奇数となる
つまり、自然数 \(m\) を用いて
\(q=2m+1\) とおける.
\(2^q=2^{2m+1}=2\times4^m≡2\times 1^m=2\)
また、\(q^2≡1\) ・・・③
(③の証明)
\(q≧5\) の素数より、\(q\) は3の倍数ではない.
つまり、自然数 \(n\) を用いて
\(q=3n±1\) とおける.
\(q^2=(3n±1)^2≡(±1)^2=1\)
したがって、②、③より
\(2^q+q^2≡2+1≡0\)
すなわち、 \(2^q+q^2\) は3の倍数
この結果と①より、\(2^q+q^2\) は素数とならない
以上、(ア)、(イ)から、\((p , q)=(2 , 3)\)
(ⅱ) \(p≧q\) のとき
(ⅰ)と同様に考え \((p , q)=(3 , 2)\)
(ⅰ)、(ⅱ)より、
\((p , q)=(2 , 3) , (3 , 2)\)
最後に
いかがだったでしょうか?
決して簡単な問題ではありませんが、この1問を通して、整数問題で大切な考え方をたくさん学ぶことが出来ます。
同じ問題は出ることはありませんが、同じ形式の問題はよく出題されるので、しっかりと考え方を理解し、自分のものにしてください。
質問等があれば気軽にコメントor問い合わせからご連絡いただけたら、数日以内には返信させていただきます。







コメント