【2018九州大学】
座標空間において,\(xy\) 平面上における双曲線 \(x^2-y^2=1\) のうち \(x≧1\) を満たす部分を \(C\) とする.また,\(z\) 軸上の点 \(A(0,0,1)\) を考える.点 \(P\) が \(C\) 上を動くとき,直線 \(AP\) と平面 \(x=d\) との交点の軌跡を求めよ.ただし,\(d\) は正の定数とする.
双曲線の媒介変数
双曲線 \(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}=1\) の媒介変数表示は
\(x=\displaystyle\frac{a}{\cos\theta}\),\(y=b\tan \theta\)
解答・解説
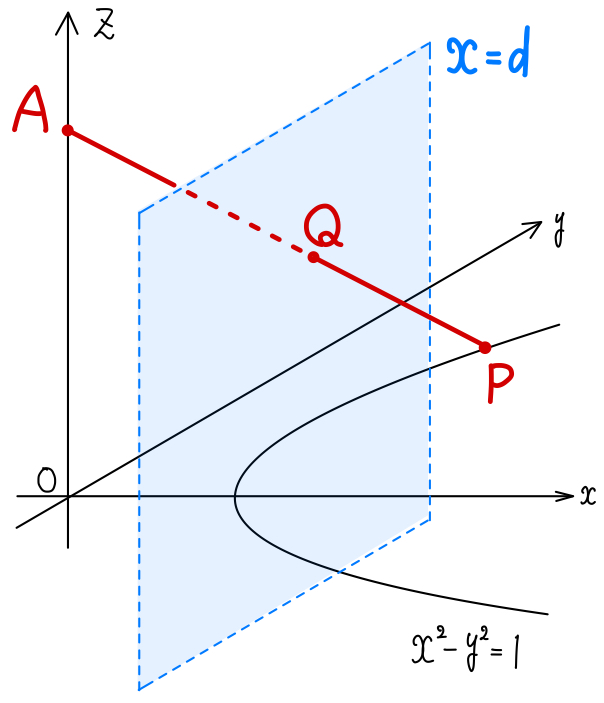
曲線 \(C\) 上の点 \(P\) は
\(P\left(\displaystyle\frac{1}{\cos \theta},\tan \theta,0\right)\) \(\left(-\displaystyle\frac{\pi}{2}< \theta<\displaystyle\frac{\pi}{2}\right)\)
とおける.
点 \(Q\) は \(AP\) 上より実数 \(k\) を用いて
\(\overrightarrow{AQ}=k\overrightarrow{AP}\)
よって,
\(\overrightarrow{OQ}=\overrightarrow{OA}+k\overrightarrow{AP}\)
\(=\left(\displaystyle\frac{k}{\cos \theta},k\tan \theta,1-k\right)\)
直線 \(AP\) と平面 \(x=d\) の交点が \(Q\) より
\(\displaystyle\frac{k}{\cos \theta}=d\) \((d>0,k>0)\)
\(k=d\cos \theta\) より
\(Q\left(d,d\sin \theta,1-d\cos \theta\right)\)
ここで \(Q\) の \(y\),\(z\) 座標を \(Y\),\(Z\) とすると,
\(Y=d\sin \theta\),\(Z=1-d\cos \theta\)
\(d>0\) より \(\sin \theta=\displaystyle\frac{Y}{d}\),\(\cos \theta=\displaystyle\frac{1-Z}{d}\)
\(\sin^2 \theta+\cos^2 \theta=1\) より
\(\left(\displaystyle\frac{Y}{d}\right)^2+\left(\displaystyle\frac{1-Z}{d}\right)^2=1\)
\(\iff\) \(Y^2+(Z-1)^2=d^2\)
また,\(-\displaystyle\frac{\pi}{2}< \theta<\displaystyle\frac{\pi}{2}\), \(\cos \theta=\displaystyle\frac{1-Z}{d}\) より
\(\displaystyle\frac{1-Z}{d}>0\) \(\iff\) \(Z<1\)
したがって求める奇跡は
\(x=d\) かつ \(y^2+(z-1)^2=d^2\),\(z<1\)







コメント