【2021大阪府立大学】絶対値を含む定積分(数学Ⅱ)の演習問題

【2021大阪府立大学】

\(a\) を正の実数とする．関数 \(S(a)=\displaystyle\int^{2}_{0}| x^2-ax |\enspace dx\) について，以下の問に答えよ．

(１)　\(x\) の関数 \(y=| x^2-ax |\) のグラフの概形をかけ．

(２)　\(S(a)\) を \(a\) を用いて表せ．

(３)　 \(a\) がすべての正の実数を動くとき，\(S(a)\) の最小値を求めよ．

解答・解説

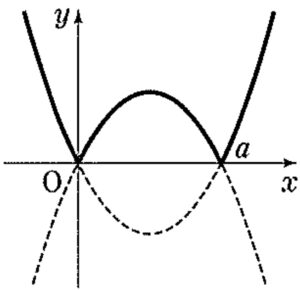\(y=| x(x-a) |\) より，グラフの概形は右図太線

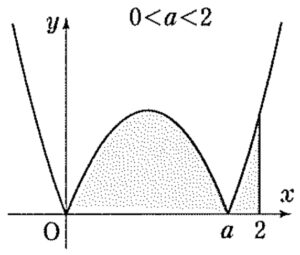( ⅰ )　\(0<a<2\) のとき

\(S(a)=\displaystyle\int^{a}_{0}(-x^2+ax) \enspace dx+\displaystyle\int^{2}_{a}(x^2-ax) \enspace dx\)

\(=-\displaystyle\int^{a}_{0}x(x-a) \enspace dx+\Bigl[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{a}{2}x^2\Bigr]^{2}_{a}\)

\(=\displaystyle\frac{1}{6}(a-0)^3+\left(\displaystyle\frac{8}{3}-2a\right)-\left(\displaystyle\frac{1}{3}a^3-\displaystyle\frac{a}{2}a^2\right)\)

\(=\displaystyle\frac{1}{3}a^3-2a+\displaystyle\frac{8}{3}\)

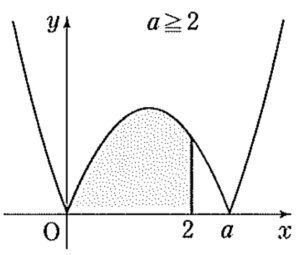( ⅱ )　\(a≧2\) のとき

\(S(a)=\displaystyle\int^{2}_{0}(-x^2+ax) \enspace dx\)

\(=\Bigl[-\displaystyle\frac{1}{3}a^3+\displaystyle\frac{a}{2}a^2\Bigr]^{2}_{0}\)

\(=2a-\displaystyle\frac{8}{3}\)

したがって，

\(S(a)=\begin{cases}\displaystyle\frac{1}{3}a^3-2a+\displaystyle\frac{8}{3}　( 0<a<2 )\\2a-\displaystyle\frac{8}{3} 　　　　　( a≧2 ) \end{cases}\)

(２)より

\(S(a)=\begin{cases}\displaystyle\frac{1}{3}a^3-2a+\displaystyle\frac{8}{3}　( 0<a<2 )\\2a-\displaystyle\frac{8}{3} 　　　　　( a≧2 ) \end{cases}\)

を \(a\) で微分すると

\(S^{\prime}(a)=\begin{cases}a^2-2　( 0<a<2 )\\2　　　　( a>2 ) \end{cases}\)

増減表は以下のようになるので

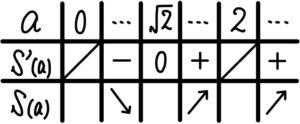
求める最小値は，\(S(\sqrt{2})=\displaystyle\frac{8-4\sqrt{2}}{3}\)