【2022大分大学・医学部・第１問】
関数 \(f(x)=\log{\displaystyle\frac{e^x}{x}}\) を用いて，\(a_{1}=2\)，\(a_{n+1}=f(a_{n})\) によって数列 \(\left\{a_{n}\right\}\) が与えられている．ただし対数は自然対数である．以下の問に答えなさい．
(１) \(1≦x≦2\) のとき，\(0≦f(x)-1≦\displaystyle\frac{1}{2}(x-1)\) が成立することを示しなさい．
(２) \(\displaystyle\lim_{n\rightarrow\infty} a_{n}\) を求めなさい．
(３) \(b_{1}=a_{1}\)，\(b_{n+1}=a_{n+1}b_{n}\) によって与えられる数列 \(\left\{b_{n}\right\}\) の極限を求めなさい．
(１)考え方・解答・解説
(１) \(1≦x≦2\) のとき，\(0≦f(x)-1≦\displaystyle\frac{1}{2}(x-1)\)
不等式の証明なので，
\(\displaystyle\frac{1}{2}(x-1)-\left\{f(x)-1\right\}\) を微分して・・・
結果的に \(1≦x≦2\) における最小値が \(0\) 以上になることを示せばいいですか？？
不等式の証明の解答の王道はそれで間違いありませんよ！
しかし今回の問題は，
『\(f(x)-1\)』『\(x-1\)』という形にぜひ注目できるようになって欲しい問題です！
平均値の定理
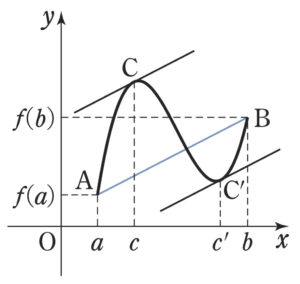関数 \(f(x)\) が閉区間 \([a,b]\) で連続で，
開区間 \((a,b)\) で微分可能ならば，
\(\displaystyle\frac{f(b)-f(a)}{b-a}=f^{\prime}(c)\) ， \(a<c<b\)
を満たす実数 \(c\) が存在する．
平均値の定理は，不等式の証明や極限を求めるときに使用されます！
差がつくテーマになりますので，常に頭の片隅には「平均値の定理」を考える癖を！
(１)解答・解説
\(0≦f(x)-1≦\displaystyle\frac{1}{2}(x-1)\) ・・・①
( ⅰ ) \(x=1\) のとき
\(f(1)-1=\log{\displaystyle\frac{e}{1}}-1=0\) ，\(\displaystyle\frac{1}{2}(1-1)=0\) より，①は成り立つ．
( ⅱ ) \(1<x≦2\) のとき
関数 \(f(x)\) は \(1≦x≦2\) で連続で，\(1<x<2\) で微分可能であるから，平均値の定理より
\(\displaystyle\frac{f(x)-1}{x-1}=f^{\prime}(c)\) ・・・②
\(1<c<2\) ・・・③ を満たす \(c\) が存在する．
ここで，\(f(x)=\log{\displaystyle\frac{e^x}{x}}=\log{e^x}-\log{x}=x-\log{x}\) より
\(f^{\prime}(c)=1-\displaystyle\frac{1}{c}\)
③より，\(\displaystyle\frac{1}{2}<\displaystyle\frac{1}{c}<1\) なので
\(0<1-\displaystyle\frac{1}{c}<\displaystyle\frac{1}{2}\)
②より，
\(0<\displaystyle\frac{f(x)-1}{x-1}<\displaystyle\frac{1}{2}\)
\(x>1\) より \(x-1>0\) なので \(0<f(x)-1<\displaystyle\frac{1}{2}(x-1)\)
したがって( ⅰ )，( ⅱ )より
\(1≦x≦2\) のとき，\(0≦f(x)-1≦\displaystyle\frac{1}{2}(x-1)\) が成立
(２)考え方・解答・解説
(２) \(\displaystyle\lim_{n\rightarrow\infty} a_{n}\)
方針が見えないときは，今までに何を求めてきたのか，どのような条件が与えられているのか(まだ使っていない条件はないか？)など考えるように！
(１)で\(0≦f(x)-1≦\displaystyle\frac{1}{2}(x-1)\)
またまだ使用していない条件として，\(a_{n+1}=f(a_{n})\) がありますね！
とりあえず，\(x=a_{n}\) を代入してみると，はさみうちの原理を利用する有名な問題に帰着します！
(２)解答・解説
数学的帰納法を用いて，自然数 \(n\) に対し，
\(0≦a_{n}-1≦\left(\displaystyle\frac{1}{2}\right)^{n-1}\) ・・・④
が成り立つことを示す．
( ⅰ ) \(n=1\) のとき
\(a_{1}-1=1\) ，\(\left(\displaystyle\frac{1}{2}\right)^0=1\) より成立．
( ⅱ ) \(n=k\) のとき④が成り立つと仮定
つまり，\(0≦a_{k}-1≦\left(\displaystyle\frac{1}{2}\right)^{k-1}\) ・・・⑤
⑤より，\(1≦a_{k}≦1+\left(\displaystyle\frac{1}{2}\right)^{k-1}≦2\) であるから，
(１)の結果に \(n=a_{k}\) を代入すると
\(0≦f(a_{k})-1≦\displaystyle\frac{1}{2}(a_{k}-1)\)
⑤より，\(0≦a_{k+1}-1≦\displaystyle\frac{1}{2}(a_{k}-1)≦\displaystyle\frac{1}{2}\cdot\left(\displaystyle\frac{1}{2}\right)^{k-1}=\left(\displaystyle\frac{1}{2}\right)^{k}\)
よって，\(0≦a_{k+1}-1≦\left(\displaystyle\frac{1}{2}\right)^{k}\) となり \(n=k+1\) のときも成り立つ．
( ⅰ )，( ⅱ )より，\(0≦a_{n}-1≦\left(\displaystyle\frac{1}{2}\right)^{n-1}\) ・・・④ が成立．
ここで，\(\displaystyle\lim_{n\rightarrow\infty}\left(\displaystyle\frac{1}{2}\right)^{n-1}=0 \) であるから，はさみうちの原理より
\(\displaystyle\lim_{n\rightarrow\infty} (a_{n}-1)=0\)
したがって，\(\displaystyle\lim_{n\rightarrow\infty}a_{n}=1\)
(３)解答・解説
\(b_{1}=a_{1}\)，\(b_{n+1}=a_{n+1}b_{n}\) より
\(b_{n}=a_{n}\cdot a_{n-1}\cdot\cdots a_{2}\cdot a_{1}\) となる．
また，\(f(x)=x-\log{x}\)，\(a_{n+1}=f(a_{n})\) より
\(a_{n+1}=a_{n}-\log{a_{n}}\)
\(=(a_{n-1}-\log{a_{n-1}})-\log{a_{n}}\)
\(\cdots\)
\(=a_{1}-(\log{a_{1}}+\cdots+\log{a_{n}})\)
\(=a_{1}-\log{(a_{1}\times \cdots \times a_{n})}\)
よって，\(a_{n+1}=2-\log{b_{n}}\) より
\(b_{n}=e^{2-a_{n+1}}\)
(２)の結果から，
\(\displaystyle\lim_{n\rightarrow\infty} b_{n}=\displaystyle\lim_{n\rightarrow\infty} e^{2-a_{n+1}}=e\)
したがって，\(\displaystyle\lim_{n\rightarrow\infty} b_{n}=e\)
コメント