【2022数学ⅠA】第2問[2](データの分析)
(1)問題と解答・解説《ケ〜ス》
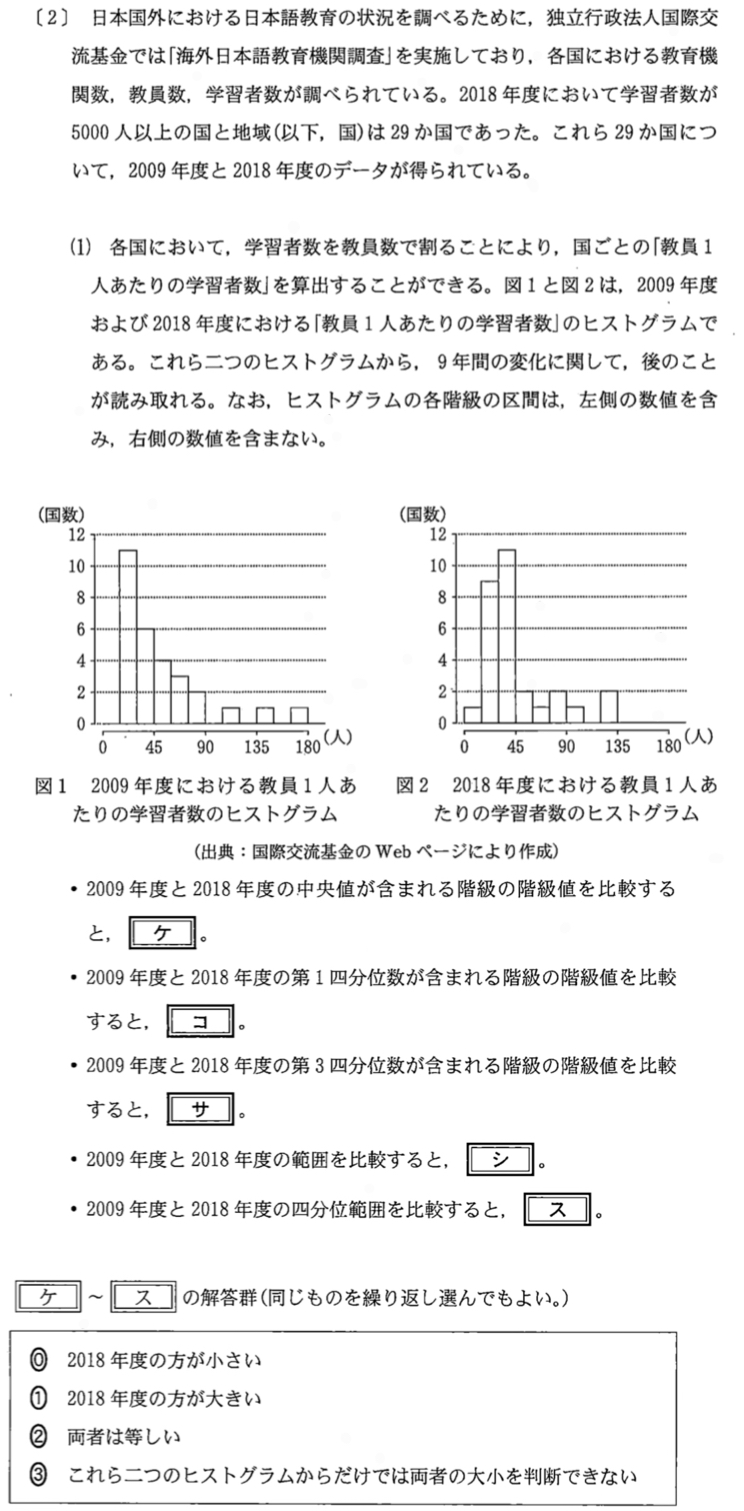
解答・解説《ケ〜ス》
\(29\) 個のデータを小さい順に並べたとき,中央値は小さい方から \(15\) 番目のデータとなる.
\(2009\) 年度と \(2018\) 年度におけるヒストグラムを比べると,中央値を含む階級はいずれも \(30\) 人以上 \(45\) 人未満で等しい.《ケ:②》
\(29\) 個のデータを小さい順に並べたとき,第 \(1\) 四分位数は小さい方から \(7\) 番目と \(8\) 番目のデータの平均となる.
第 \(1\) 四分位数を含む階級はいずれも \(15\) 人以上 \(30\) 人未満で等しい.《コ:②》
\(29\) 個のデータを小さい順に並べたとき,第 \(3\) 四分位数は大きい方から \(7\) 番目と \(8\) 番目のデータの平均となる.
第 \(3\) 四分位数を含む階級は,\(2009\) 年度が \(60\) 人以上 \(75\) 人未満,\(2018\) 年度が \(45\) 人以上 \(60\) 人未満である.《サ:⓪》
範囲とは,データの最大値と最小値の差であるから,
\(2009\) 年度が \(165-29=136\) 人以上,\(2018\) 年度が \(134-0=134\) 人以下となる.《シ:⓪》
四分位範囲とは,第 \(3\) 四分位数と第 \(1\) 四分位数の差であるから,
\(2009\) 年度が \(60-29=31\) 人以上 \(74-15=59\) 人以下,
\(2018\) 年度が \(45-29=16\) 人以上 \(59-15=44\) 人以下.
これだけでは大小を判断できない.《ス:③》
(2)問題と解答・解説《セ》
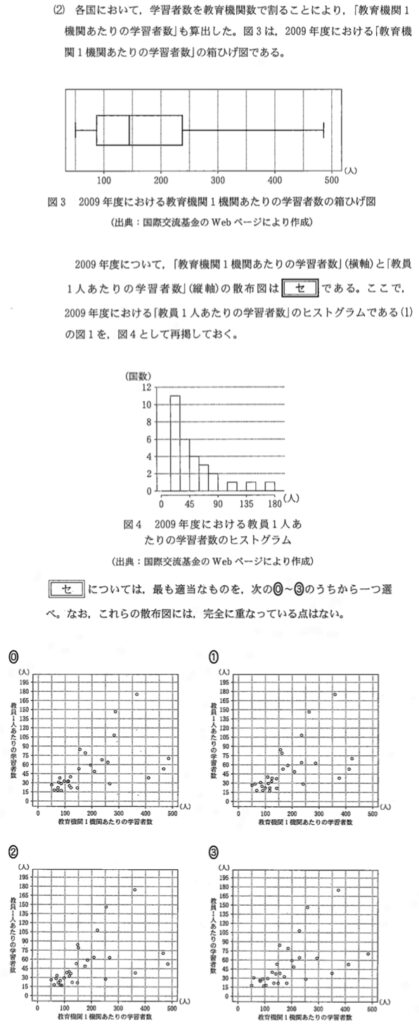
解答・解説《セ》
箱ひげ図から次のことが読み取れる.
・中央値は \(150\) 人未満
・第 \(1\) 四分位数は \(100\) 人未満
・第 \(3\) 四分位数は \(250\) 人未満
・最大値は \(450\) 人以上
これと散布図を比べると,
⓪は \(250\) 人以上のデータが \(8\) 個あるため,第 \(3\) 四分位数は \(250\) 人未満であることに反する.
①は最大値が \(450\) 人未満であるため不適
②は条件を満たす
③は \(100\) 人以下のデータが \(6\) 個あるため,第 \(1\) 四分位数は \(100\) 人未満であることに反する.
したがって,《セ:②》
(3)問題と解答・解説《ソ〜チ》

解答・解説《ソ〜チ》
\(S\) と \(T\) の相関係数は,\(\displaystyle\frac{SとTの共分散}{(Sの標準偏差)(Tの標準偏差)}\) であるから,
\(\displaystyle\frac{735.3}{39.3\times 29.9}=0.625\cdots\)
小数第 \(3\) 位を四捨五入して, \(0.63\) ・・・《ソ〜チ》
(4)問題と解答・解説《ツ》
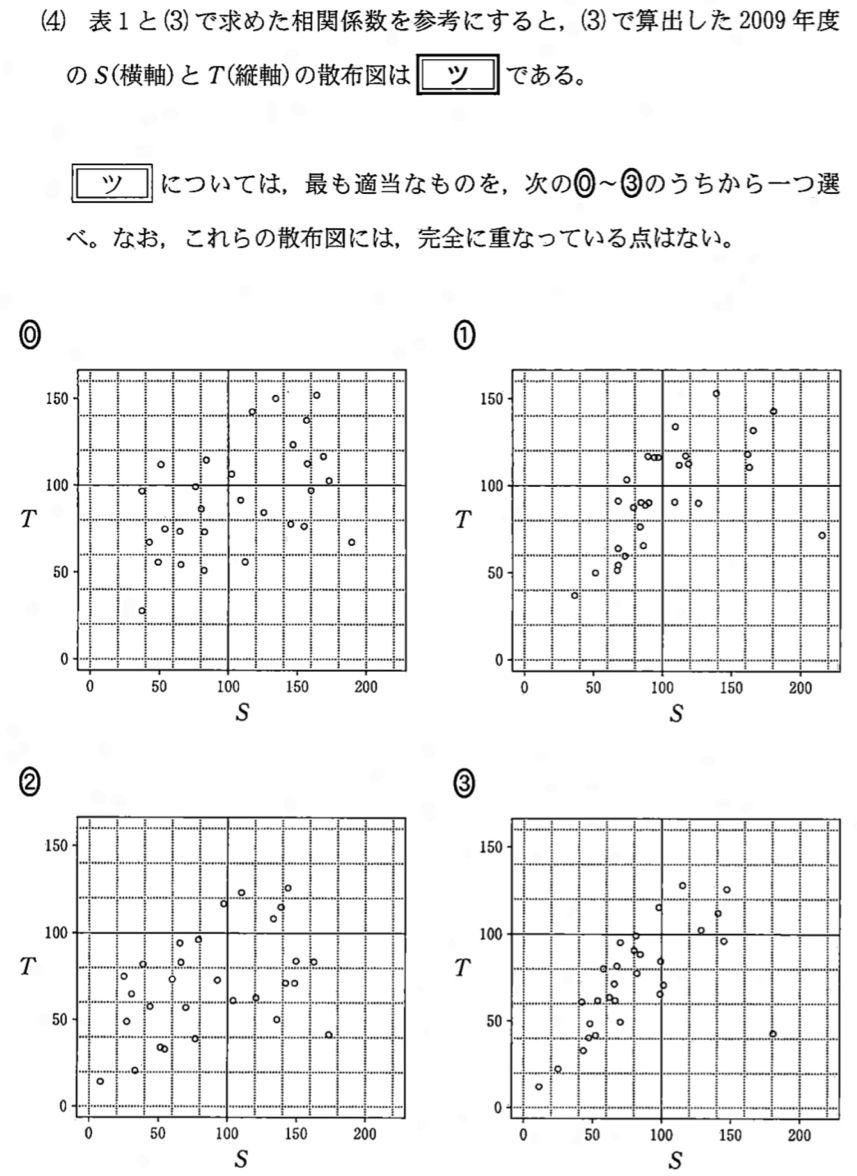
解答・解説《ツ》
(3)で求めた相関係数の値が \(0.63\) であることから,やや強い正の相関があることがわかる.
よって適切な散布図は①または③である.
①の散布図に注目すると,\(T\) の値が \(80\) を超えるデータが \(20\) 個,\(80\) を下回るデータが \(9\) 個の分布から考えて,データの平均値は明らかに \(80\) を超えることがわかる.よって平均値が \(72.9\) となることはあり得ない.
したがって,《ツ:③》









コメント