【2021三重大学・教育,工(後期)】
\(z^3=-\overline{z^3}\) で,\(z^3\) の虚部が \(0\) より大きく \(27\) より小さいような複素数 \(z\) の全体を図示せよ.
Point:実数・虚数条件
・\(z\) が実数 \(\iff\) \(\overline{ z } = z\)
・\(z\) が純虚数 \(\iff\) \(\overline{ z } = -z\)、\(z\not=0\)
解答・解説
\(z^3\not=0\),\(z^3+\overline{z^3}=0\) より,\(z^3\) は純虚数となる.
\(z=r(\cos\theta+i\sin \theta)\) ( \(r>0\),\(0≦\theta<2\pi\) ) とおく.
\(z^3=r^3(\cos 3\theta+i\sin 3\theta)\)
\(z^3\) の虚部が \(0\) より大きく \(27\) より小さいことから
\(0<r^3<27\) ,\(\cos 3\theta=0\) ,\(\sin 3\theta=1\)
よって,\(0<r<3\) ・・・①
また,\(0≦3\theta<6\pi\) より
\(3\theta=\displaystyle\frac{\pi}{2},\displaystyle\frac{5\pi}{2},\displaystyle\frac{9\pi}{2}\)
よって,\(\theta=\displaystyle\frac{\pi}{6},\displaystyle\frac{5\pi}{6},\displaystyle\frac{3\pi}{2}\) ・・・②
したがって,①,②を満たす複素数 \(z\) の全体は右図(赤線部分)のようになる.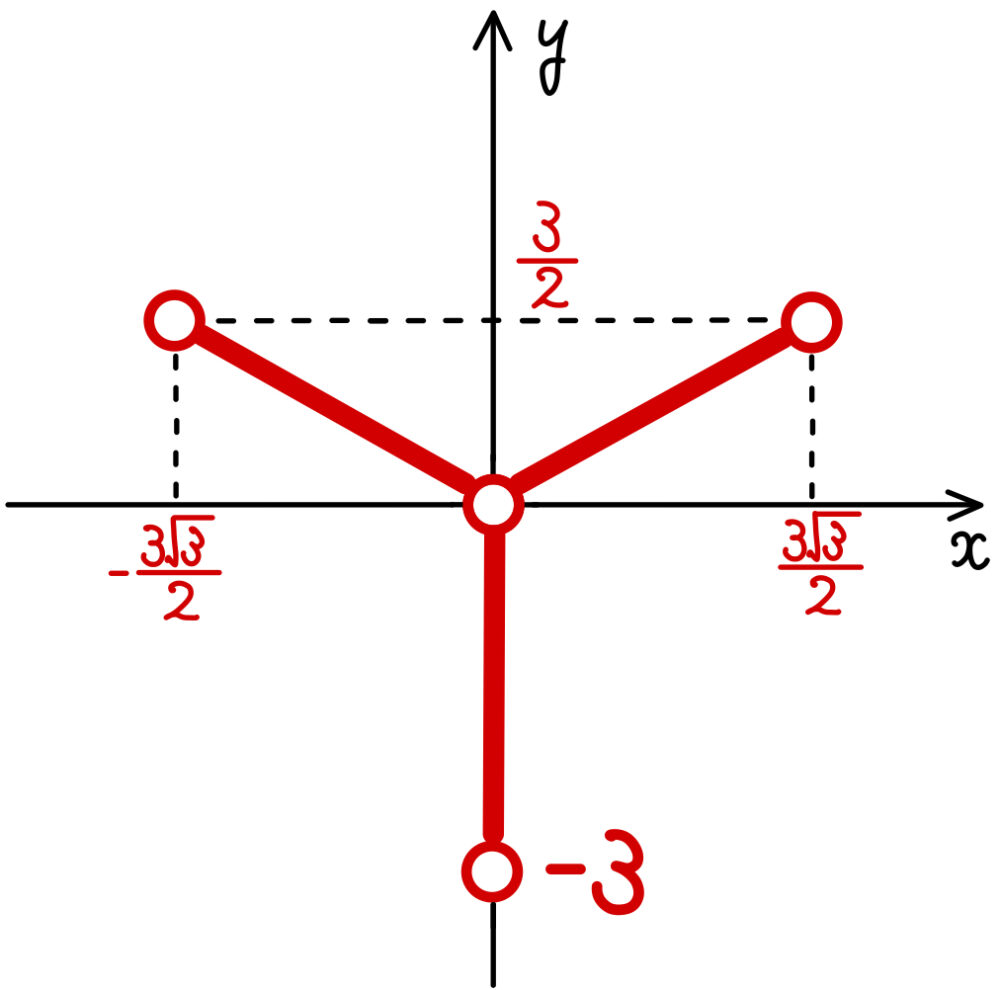








コメント