【2022一橋大学(後期)】
\(\log_{y}{(6x+y)}=x\) を満たす正の整数 \(x\) , \(y\) の組を求めよ.
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
考え方・解答・解説

対数の問題ですから,底や真数条件などから
\(x\) , \(y\) の範囲を絞りましょう!
底の条件より, \(y>0\) , \(y\not=1\) で
\(y\) は正の整数より,\(y≧2\)
\(\log_{y}{(6x+y)}=x\)
\(\iff\) \(6x+y=y^x\)
\(6x=y(y^{x-1}-1)\) ・・・①
\(x=1\) のとき①より \(6=0\) となり不適
よって \(x\not=1\)
\(x\) は正の整数より,\(x≧2\)

\(x≧2\) , \(y≧2\) は分かったけど,思ったよりも範囲が絞れなかった・・・

次に①の形に注目してみましょう!
左辺は \(1\) 次式,右辺は指数関数で \(x≧2\) より両辺ともに単調増加な関数!!
\(x\) , \(y\) の値が大きくなると,①は右辺の値の方が大きくなることがわかりますね!
つまり,\(x\) も \(y\) もある程度小さい値であることが予想されるので,順に実験していきましょう!
\(x≧2\) のとき
\(y(y^{x-1}-1)\) は \(y\) の単調増加な関数なので \(y≧2\) より
\(6x=y(y^{x-1}-1)≧2(2^{x-1}-1)\)
よって,\(3x≧2^{x-1}-1\) ・・・②
を満たす必要がある.
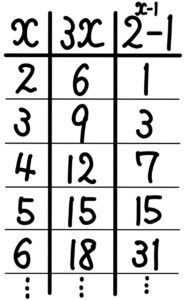
②を満たす \(x\) は \(2≦x≦5\)
( ⅰ ) \(x=2\) のとき
①より \(12=y(y-1)\)
\(y^2-y-12=0\)
\((y+3)(y-4)=0\)
\(y≧2\) より \(y=4\)
( ⅱ ) \(x=3\) のとき
①より \(18=y(y^2-1)\)
・\(y=2\) のとき,\(18>2(2^2-1)\)
・\(y≧3\) のとき
\(y(y^2-1)≧3(3^2-1)=24>18\) となり
これを満たす自然数 \(y\) は存在しない
( ⅲ ) \(x=4\) のとき
①より \(24=y(y^3-1)\)
・\(y=2\) のとき,\(24>2(2^3-1)\)
・\(y≧3\) のとき
\(y(y^3-1)≧3(3^3-1)=78>24\) となり
これを満たす自然数 \(y\) は存在しない
( ⅳ ) \(x=5\) のとき
①より \(30=y(y^4-1)\)
・\(y=2\) のとき成立する.
・\(y≧3\) のとき
\(y(y^4-1)≧3(3^4-1)=240>30\) となり
これを満たす自然数 \(y\) は存在しない
以上より,\((x,y)=(2,4),(5,2)\)







コメント