2022北海道大学・理・第４問【確率】同じ文字を含む円順列・条件付き確率

考え方

場合の数と円順列の違い

細かな違いを言い出せばきりがありませんが、問題を解いていく上で最も重要な違いとしては、

場合の数・確率が苦手な方の多くは、ただただ公式に当てはめようとしたり、基本的な違いを理解していないことがほとんどです。また、ある一定以上の点数が取れない方の多くも、意外とそのような基本的な違いを理解していないケースが多いです。

場合の数・確率に対して、少しでも苦手意識を持っている人は、現時点での確率の点数に関わらず、一度、安田亨の「ハッとめざめる確率」に取り組んで見て下さい。

この１冊で、場合の数・確率に対する考え方の基礎基本を身に付けることができ、そして発展問題への考え方を身に付けることができます！

円順列

※回転して一致するものは同じものであると考えるため、\(1\) 文字を固定して、その他のものを今まで通りに並べる．

条件付き確率

解答

(１)

すべての玉を区別して考える．

つまり、\(O\) については、\(O_{1}\)、\(O_{2}\)、

\(K\) については、\(K_{1}\)、\(K_{2}\) として考える．

このとき、異なる \(8\) 個の玉で円順列をつくる総数は、

\((8-1)!=7!\) 通り

この中で、時計回りに「\(ＨＯＫＫＡＩＤＯ\)」と並ぶのは、

\(O_{1}\)、\(O_{2}\) と \(K_{1}\)、\(K_{2}\) の並び替えを考えた

\(2!\times2!\) 通り

したがって求める確率は、\(\displaystyle\frac{2!\times2!}{7!}=\displaystyle\frac{1}{1260}\)

(２)

子音が隣り合わない場合を考える．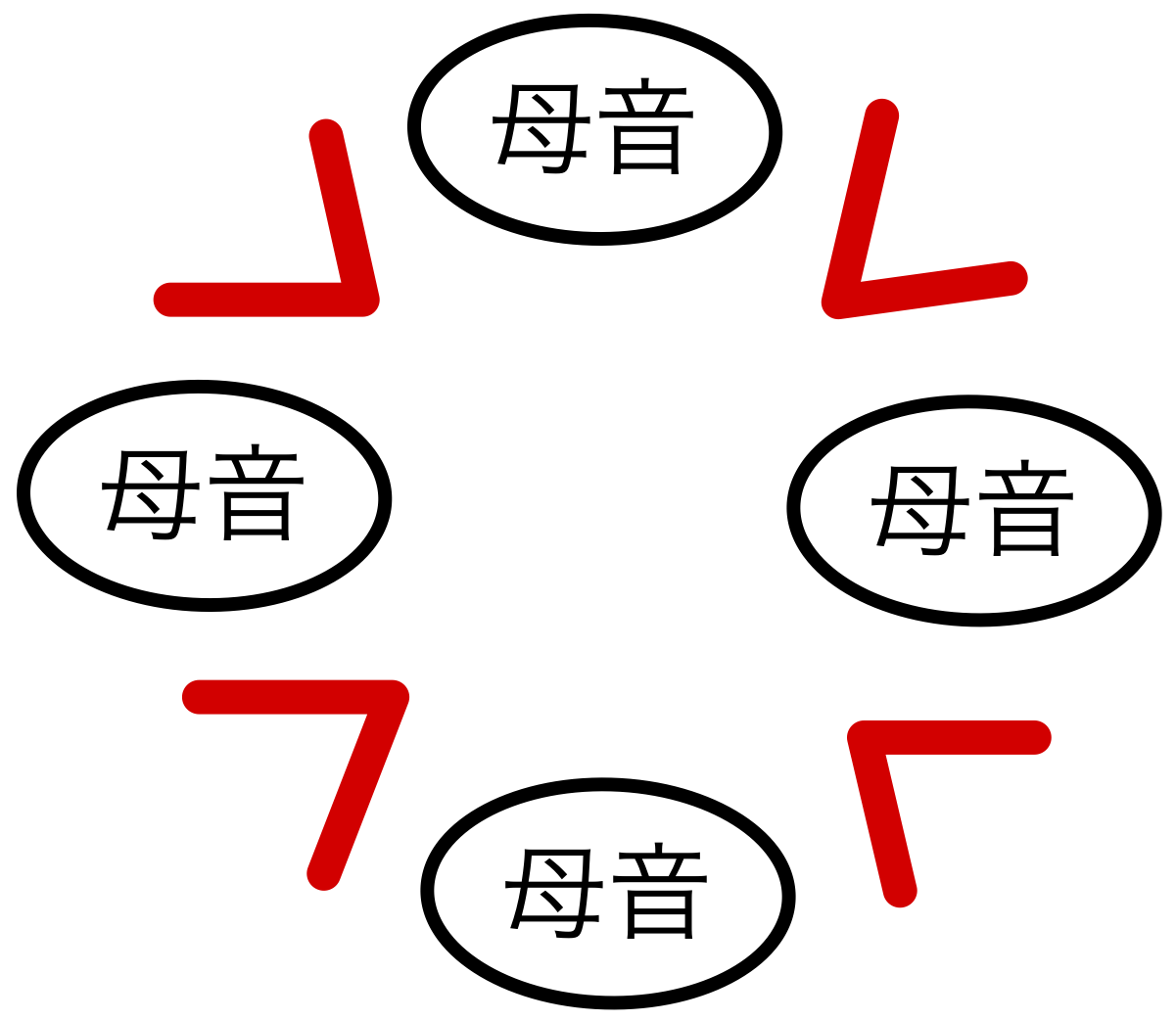

母音の\(O_{1}\)、\(O_{2}\)、\(A\)、\(I\) の異なる \(4\) 個の円順列の総数は

\((4-1)!=3!\) 通り

次に、子音が隣り合わないとき、上で並べた \(4\) 個の玉の間の \(4\) カ所に子音の \(H\)、\(K_{1}\)、\(K_{2}\)、\(D\) を \(1\) つずつ並べていけばよいので、子音の並べ方は \(4!\) 通り

したがって、子音が隣り合わない確率は、\(\displaystyle\frac{3!\times4!}{7!}=\displaystyle\frac{1}{35}\) であるから、

求める確率は、\(1-\displaystyle\frac{1}{35}=\displaystyle\frac{34}{35}\)

(３)

子音の \(K_{1}\)、\(K_{2}\) だけが隣り合うときを考える．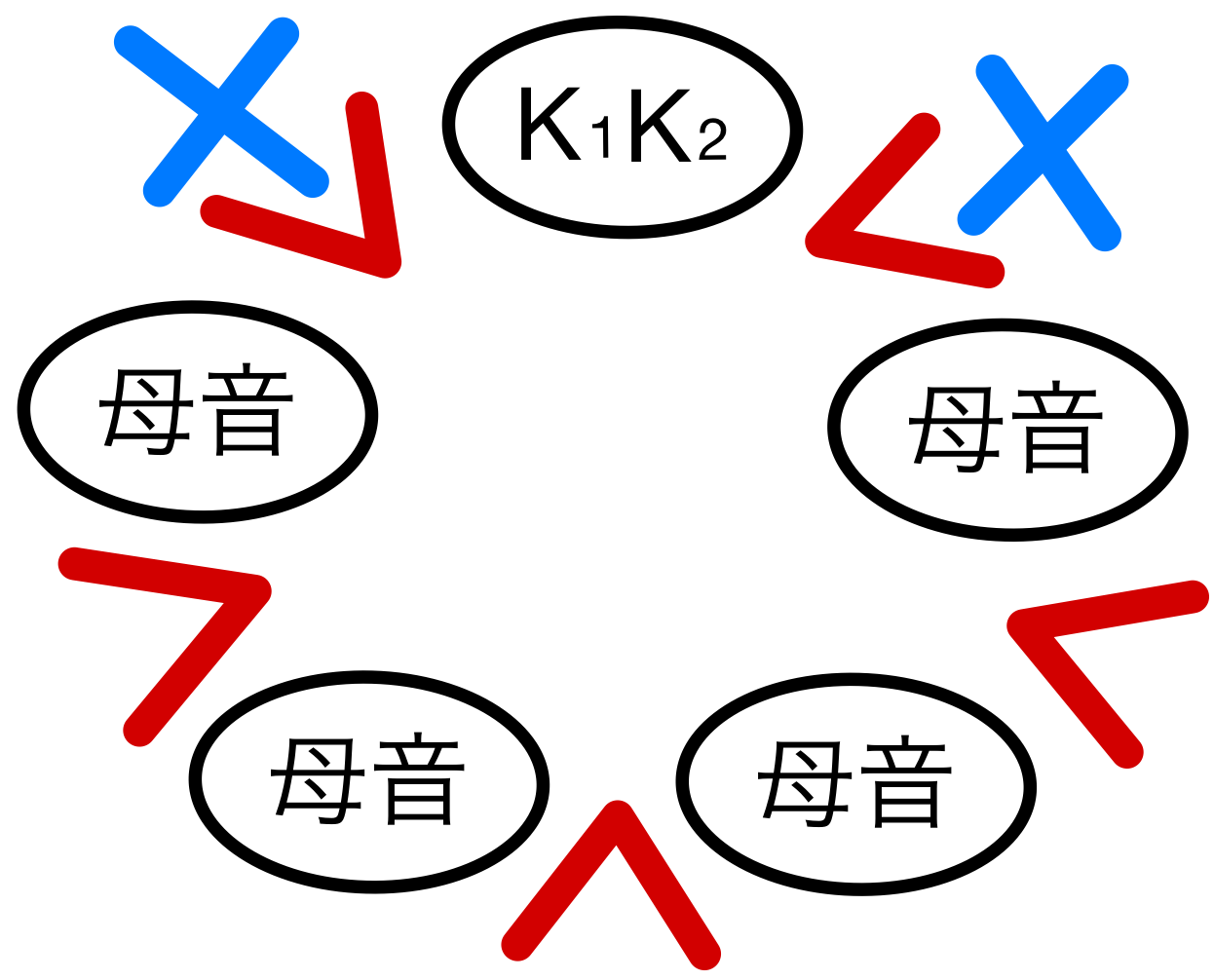

\(2\) 文字 \(K_{1}K_{2}\) を固定し、母音の\(O_{1}\)、\(O_{2}\)、\(A\)、\(I\) の異なる \(4\) 個を並べると、\(4!\) 通り

また、\(K_{1}K_{2}\)、\(K_{2}K_{1}\) の \(K\) についての並び方が \(2\) 通り．

さらに、上で並べた玉の間 \(3\) カ所 ( \(K_{1}\)、\(K_{2}\) のとなり以外 ) から \(2\) カ所選んで、\(H\)、\(D\) を並べればよいので、\(H\)、\(D\) の並べ方は \(_{3}P_{2}\) 通り

したがって子音の \(K_{1}\)、\(K_{2}\) だけが隣り合う確率は、

\(\displaystyle\frac{4!\times2!\times_{3}P_{2}}{7!}=\displaystyle\frac{2}{35}\)

であるから、求める条件付き確率は、\(\displaystyle\frac{\displaystyle\frac{2}{35}}{\displaystyle\frac{34}{35}}=\displaystyle\frac{1}{17}\)