 【2022慶應義塾大学】
【2022慶應義塾大学】
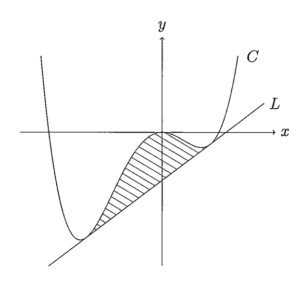
\(xy\) 平面上の曲線 \(C\) を \(y=x^2(x-1)(x+2)\) とする.
(1) \(C\) に \(2\) 点で下から接する直線 \(L\) の方程式を求めよ.
(2) \(C\) と \(L\) が囲む図の斜線部分の面積を求めよ.
(1) 考え方・解答
求める接線 \(L\) を \(y=ax+b\) とおく.
\(x^2(x-1)(x+2)=ax+b\)
\(x^4+x^3-2x^2-ax-b=0\) ・・・①
ここで,①の解が \(C\) と \(L\) の接点の \(x\) 座標を表すので,接点の \(x\) 座標を \(\alpha\),\(\beta\) ( \(\alpha<\beta\) ) とおくと
\(x^4+x^3-2x^2-ax-b=(x-\alpha)^2(x-\beta)^2\) ・・・②
\((x-\alpha)^2(x-\beta)^2=x^4-2(\alpha+\beta)x^3+(\alpha^2+4\alpha\beta+\beta^2)x^2-2(\alpha\beta^2+\alpha^2\beta)x+\alpha^2\beta^2\)
であるから②より係数を比較して
\(1=-2(\alpha+\beta)\) ・・・①
\(-2=\alpha^2+4\alpha\beta+\beta^2\) ・・・②
\(-a=-2(\alpha\beta^2+\alpha^2\beta)\) ・・・③
\(-b=\alpha^2\beta^2\) ・・・④
①より,\(\alpha+\beta=-\displaystyle\frac{1}{2}\) ・・・⑤
②より,\((\alpha+\beta)^2+2\alpha\beta=-2\)
⑤を代入すると,\(\alpha\beta=-\displaystyle\frac{9}{8}\) ・・・⑥
⑤,⑥より \(\alpha\),\(\beta\) は
\(t^2+\displaystyle\frac{1}{2}t-\displaystyle\frac{9}{8}=0\)
つまり,\(8t^2+4t-9=0\) の \(2\) 解を表すので,
\(t=\displaystyle\frac{-1\pm\sqrt{19}}{4}\)
よって,\(\alpha=\displaystyle\frac{-1-\sqrt{19}}{4}\),\(\beta=\displaystyle\frac{-1+\sqrt{19}}{4}\)
また③より
\(a=2\alpha\beta(\alpha+\beta)=\displaystyle\frac{9}{8}\)
④より
\(b=-\left(-\displaystyle\frac{9}{8}\right)^2=-\displaystyle\frac{81}{64}\)
したがって求める直線 \(L\) は,\(y=\displaystyle\frac{9}{8}x-\displaystyle\frac{81}{64}\)
(2) 考え方・解答

4次関数と二重接線で囲まれた図形の面積公式です!
有名な公式ですので,結論は覚えておきましょう!
その上で,下記に示す記述の解答の流れも作れるように!

求める面積 \(S\) は
\(S=\displaystyle\int^{\beta}_{\alpha}\left\{x^2(x-1)(x+2)-(ax+b)\right\}dx\)
\(=\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^2(x-\beta)^2dx\)
\(=\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^2\left\{(x-\alpha)-(\beta-\alpha)\right\}^2dx\)
\(=\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^2\left\{(x-\alpha)^2-2(\beta-\alpha)(x-\alpha)+(\beta-\alpha)^2\right\}dx\)
\(=\displaystyle\int^{\beta}_{\alpha}\left\{(x-\alpha)^4-2(\beta-\alpha)(x-\alpha)^3+(\beta-\alpha)^2(x-\alpha)^2\right\}dx\)
\(=\Bigl[\displaystyle\frac{1}{5}(x-\alpha)^5-\displaystyle\frac{1}{2}(\beta-\alpha)(x-\alpha)^4+\displaystyle\frac{1}{3}(\beta-\alpha)^2(x-\alpha)^3\Bigr]^{\beta}_{\alpha}\)
\(=\displaystyle\frac{1}{5}(\beta-\alpha)^5-\displaystyle\frac{1}{2}(\beta-\alpha)^5+\displaystyle\frac{1}{3}(\beta-\alpha)^5\)
\(=\displaystyle\frac{1}{30}(\beta-\alpha)^5\)
(1)の結果から \(\alpha=\displaystyle\frac{-1-\sqrt{19}}{4}\),\(\beta=\displaystyle\frac{-1+\sqrt{19}}{4}\) より
\(\beta-\alpha=\displaystyle\frac{\sqrt{19}}{2}\) より
\(S=\displaystyle\frac{1}{30}\left(\displaystyle\frac{\sqrt{19}}{2}\right)^5=\displaystyle\frac{361\sqrt{19}}{960}\)








コメント